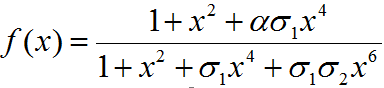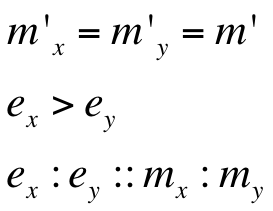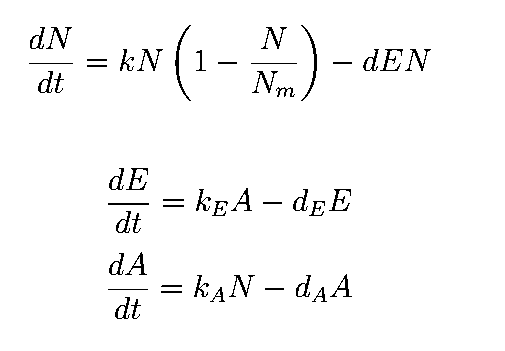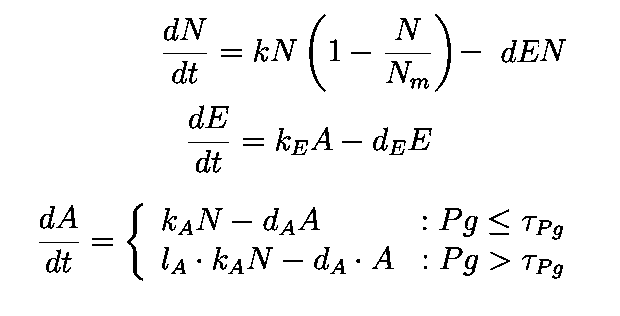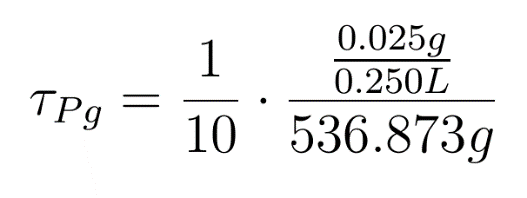Team:IISER Pune/Modeling

Your browser does not support the canvas tag.

Top

---

Introduction

Mathematical modeling suffices to –

• Provide an objective view towards complex & apparently diverse systems. This objectivity is instrumental for efforts motivated by the idea of generalization.


• Provide an ability to predict the behavior of a system i.e. to predict the properties of a state of the system given the information for some other state.

Simulations–

• Give us a way in which the numbers mimic biological/chemical ‘characters’ & equations derive their behavior.

• Help us in visualizing the results of equations that are analytically unsolvable.

Here, with the instruments of ODEs, two biological circuits were modeled (and solved!)

1. Variable-link Oscillator - Hijack Module
2. Killer gene Circuit – Termination Module

Software & Methods

For solving the ODE (Ordinary Differential Equations) – Python 2.7.10 was used. We have used the Anaconda (Python distribution) for running all our scripts.

Initially we wrote our own implementation of Euler’s method of integration to solve all the systems of equations.

But after learning about scipy.integrate module we have been using Scipy's odeint function for integrating the ODEs

Scipy [version 0.15.1]

Modelling

---

Variable-link Oscillator

Description of oscillator

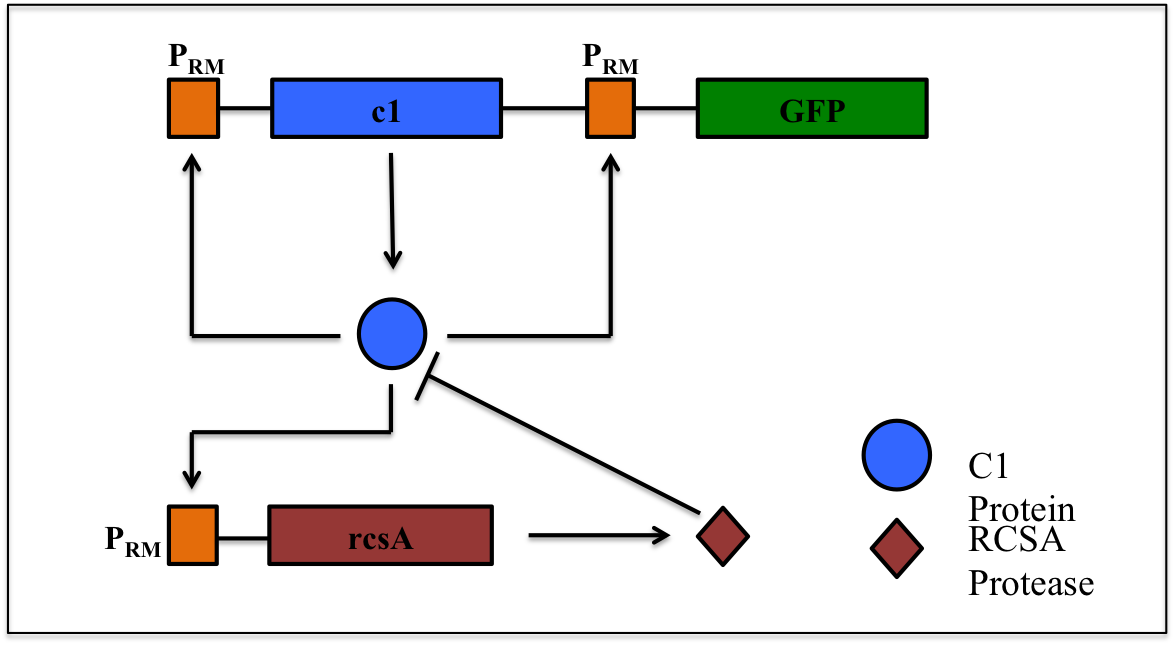
This is a synthetic genetic oscillator, operative in bacteria, first described by Hasty et. Al (ref. 1). The regulation here is based on protein- protease interaction between cI (protein responsible for maintaining lysogenous state in acteria infected with lambda phage) & rcsA (bacterial protease specific to cI). The cI protein acts as an auto-activator & an activator for production of rcsA while rcsA acts for degradation of cI, after a certain concentration of cI has been achieved. Hence, the concentration of cI exhibits oscillations. The behavior of these oscillations can be enquired when a visible reporter (like GFP) is incorporated in the network.

The basic requirement of the network is that all the genes- the cI gene, the rcsA gene & the gfp gene, should be present under the activity of same promoter – P_RM (the natural promoter of cI in lambda phage).

The original model

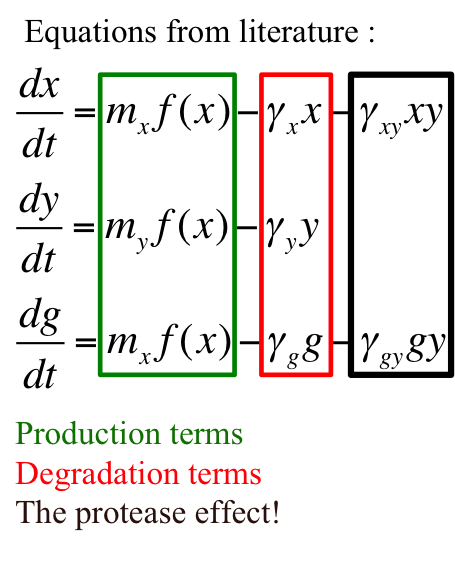
The model for this oscillator is formulated in the form of system of coupled ODEs.

where

Introduction to variables:

'

Symbol	Parameter
x	[CI]
y	[RCSA]
g	[GFP]
mx	copy number of plasmid containing cI gene
my	copy number of plasmid containing rcsA gene
γx	rate constant for natural degradation of cI
γy	rate constant for natural degradation of rcsA
γg	rate constant for natural degradation of gfp
γxy	rate constant for natural degradation of cI due to protease activity
γgy	rate constant depicting no depletion in production of gfp as a consequence of protease activity on activator - cI
f(x)	function determining production of gene under promoter PRM
σ1	Coefficient for binding of cI to OR2 relative to OR1
σ2	Coefficient for binding of cI to OR3 relative to OR1

Figure 1.2 Schematic describing activity under promoter P_RM

P_RM promoter has three operator sites- OR1, OR2, OR3 to which CI-dimer binds sequentially. Binding of CI to OR2 enhances transcription & that to OR3 represses transcription.

Assumptions of Model –

1. The cI gene along with reporter (gfp) gene is present on one plasmid, say – x, with plasmid copy number – mx, while the rcsA gene is present on another plasmid, say – y, with plasmid copy number – my . The oscillator is actualized as a two-plasmid system.
2. (Major assumption)
   m_x > m_y
   This assumption is responsible for maintaining the oscillatory nature of the system.
3. Reactions like transcription & normal degradation are slow & irreversible. Degradation is essentially due to growth.

Our work

Imitation

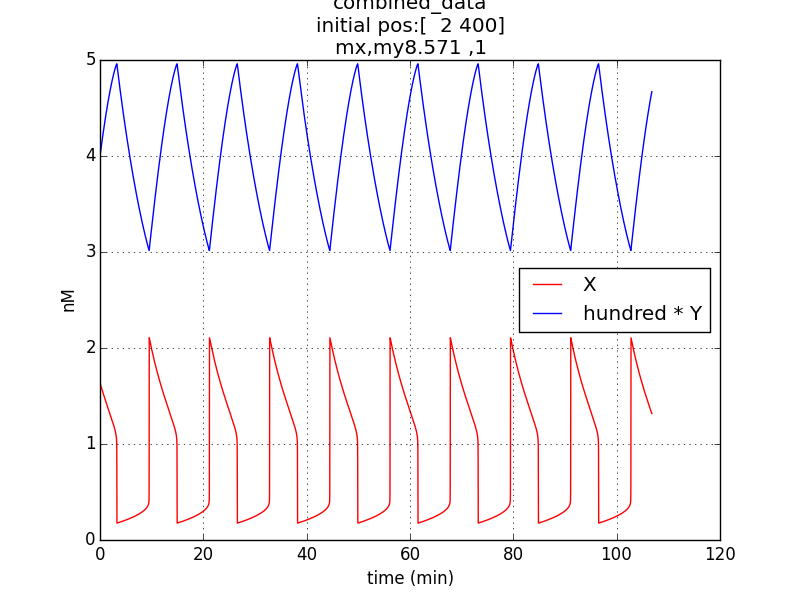
Reproduction of result- to be able to show oscillations (in x & y; here g is not considered separately since its behavior would be similar to that of x) through simulation has been possible by employing specific parametric values referred from literature (ref.1, ref.2).

Conditions for simulation:

Table 1.1

Symbol	Value
x-initial conc.	4 nM
y-initial conc.	200 nM
mx	10
my	1
γx	0.1
γy	0.01
γxy	0.1
α	11
σ1	2
σ2	0.08

Figure 1.3 Concentration (nM) v/s time (min) plot to depict oscillations in case of original model

Oscillations (according to model equations) of period of about 1o minutes were obtained on simulating the specified conditions.

Investigation

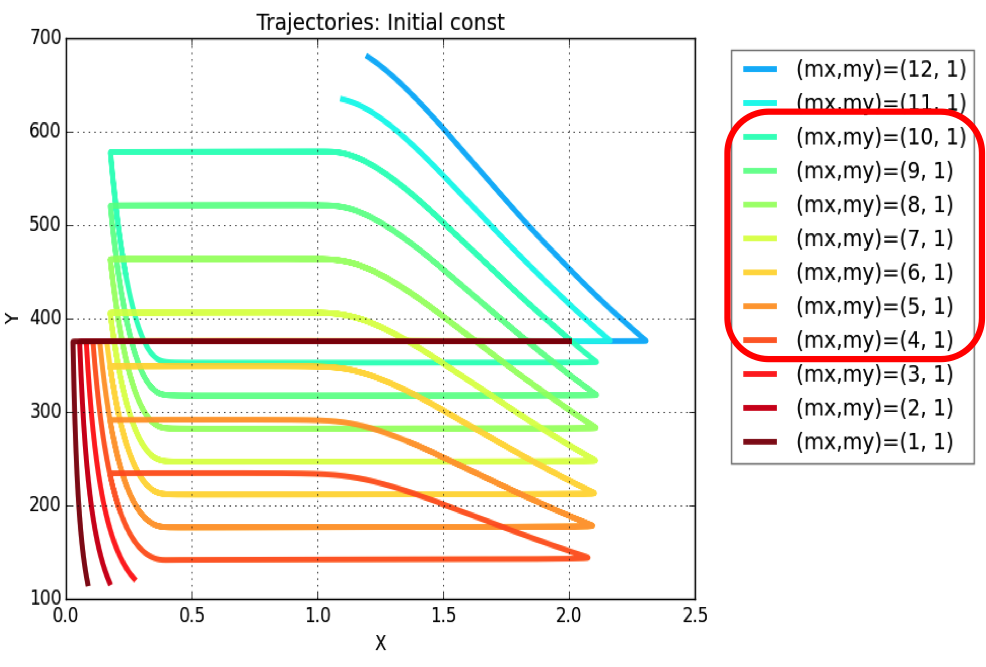
Plasmid copy number is an evident parameter when tunability of the oscillator is considered. Keeping the values of all other variables constant, simulations were run for exploring those values of mx & my, for which system exhibits oscillatory regime.

Figure 1.4 Phasor diagram for concentration of y v/s x for different values of (mx,my)

The simulation leads to conclusion that oscillations are possible for a range of plasmid copy number ratio (mx : my) values as marked in the legend of the plot. Oscillations (of varying amplitudes & periods) occur between mx : my = 4:1 & mx : my = 10:1.

Innovation

Employing this oscillator in our genetic device is possible only at the cost of violating the major assumption of this model- mx > my . This is because our entire genetic device needs to be packaged in single plasmid vector & hence, two plasmid based oscillator is not feasible.

This problem led to development of alternative strategies to create a single plasmid based oscillator. The basic idea behind these strategies is to exploit other parameters like- RBS efficiency, number of gene sets etc. to achieve the same numerical ratio for which oscillatory regime exists.

Alternative strategies :

1. Multiple promoter sites (i.e. gene sets)-
   • Disadvantages of this alternative :
     • Not “effective” as plasmid copy no. ratio
     • Possible problems arising due to promoter titration
     • Requirement of larger plasmids
2. Different RBS Efficiency ratios-
   • Advantages of this alternative :
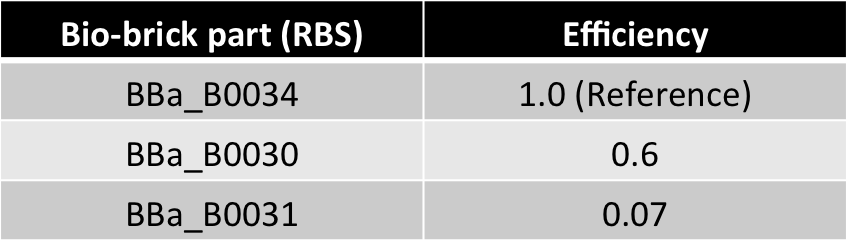
     • Present as bio-bricks (measurements performed)
     • Efficiency ratios comparable in magnitude to copy no. ratio (from 4:1 to 10:1)

3. Combinatorial way-

(no. of gene sets) * (RBS efficiency ratio) ≅ plasmid copy no.

Here, our model is an oscillator that exploits the difference in the translational efficiencies of different ribosome binding sites (RBSs).Our model makes use of existing, well characterized RBSs (present as bio-bricks) whose efficiencies are known.

Introduction to new variables : e_x = RBS efficiency of RBS associated with cI gene

e_y = RBS efficiency of RBS associated with rcsA gene

m’ = plasmid copy number of the ‘single’ plasmid (containing entire oscillator)

Assumptions of our model :

The simulation run :

Table 1.2 RBSs of different efficiencies as Bio-bricks

Conditions for simulation

Table 1.3

Symbol	Value
ex	0.6
ey	0.07
m' = mx' = my'	10

Keeping all other parameters at same values as in Table 1.1

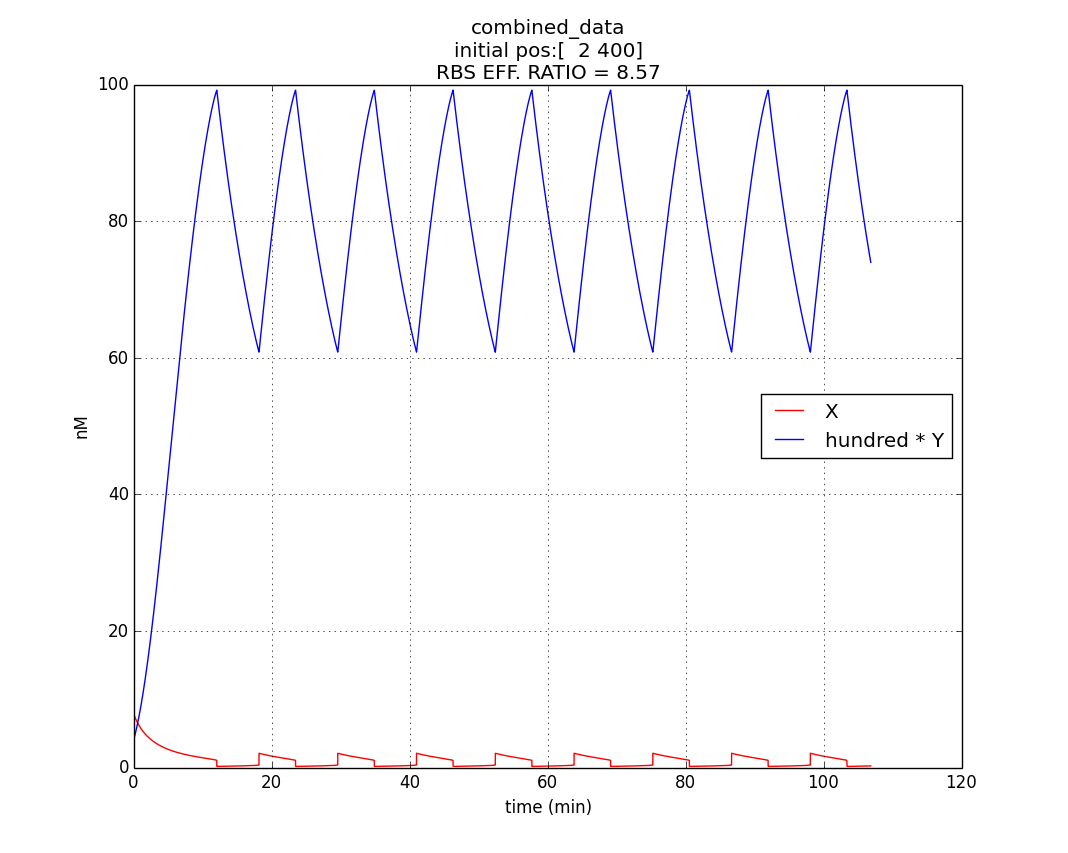
Hence, ex : ey = 0.6 : 0.07 = 8.75 : 1 (which is between 4:1 & 10:1 numeric ratio values)

Figure 1.6Concentration (nM) v/s time (min) to depict oscillations in case of our model

The simulation run for specific RBS efficiency ratio, keeping all other parameters consistent with the first simulation, resulted in oscillations of period- 10 minutes. Hence, efficient oscillations are shown by our model with respect to period (which is crucial to our genetic device).


Concluding Remarks

1. Successful in reproducing the published results for variable-link oscillator.
2. Successful in exploring the parametric range for which oscillatory regime exists.
3. Successful in building a general strategy for designing a single plasmid based oscillator.
4. Successful in showing oscillations of a single plasmid based oscillator harnessing different RBS efficiencies.

References

1. Designer Gene Networks : Towards Fundamental Cellular Control -- J. Hasty & et.al.

2. Comparative analysis of synthetic genetic oscillators -- O. Purcell & et.al.

---

Quorum Sensing Termination Circuit

Introduction

The termination module to self destruct cells or cease further replication and thus to prevent uncontrolled growth is a necessity of our genetic device, considering the bio-safety of the whole project.

Background

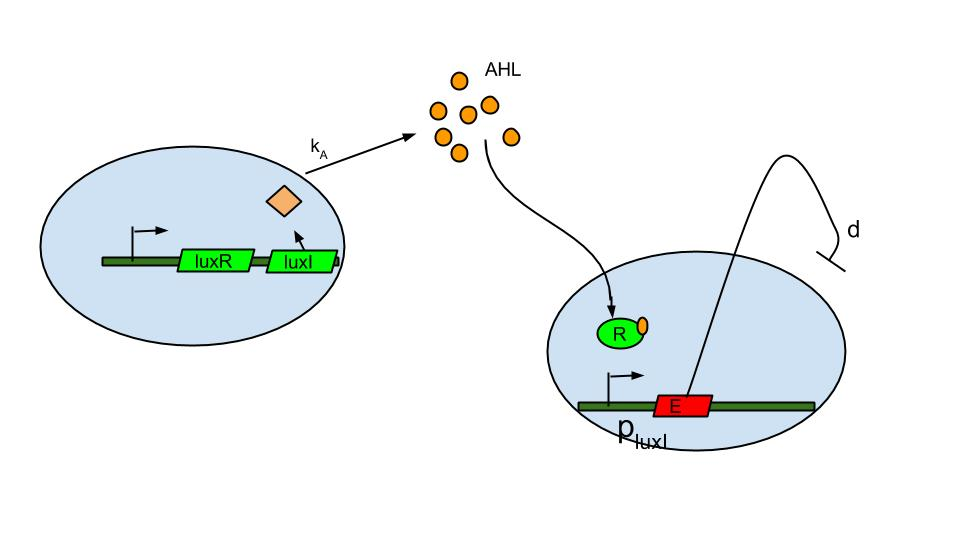
Quorum sensing is well known in the form of luxI/luxR system which was found in Vibrio fischeri a marine bacterium. The bacterium is known to release signaling molecule AHL (acyl-homoserine lactone) which diffuses across the cell membrane. As cell density increases AHL concentration increases in the extracellular medium and inside the cells. At high enough concentrations it binds to and activates LuxR, a transcriptional regulator which then induces the LuxI promoter causing the expression of fluorescent protein.

The basic termination model has been described and demonstrated earlier based on lux R-lux I system (ref.1). The system comprises of sender and receiver parts wherein, promoter of sender part is IPTG inducible. When the promoter is switched on.

1. luxI production causes release of AHL .
2. The AHL diffuses across cell membranes to nearby cells and binds to luxR.
3. Activated luxR induces the plux I releasing the Ccdb toxin (E) that causes cell death.

Model

The first approach was to have the termination module switched on from the start, sending the AHL signals.

Figure 2.1 Basic Quorum Sensing Terminator Module. On IPTG induction the luxR is switched on producing luxI (orange diamond). LuxI results in production of AHL (orange circles) which diffuses out of the cell. The free AHL binds to luxR activating it.

In this the model previously proposed (You et. al. 2004 ) was successfully reproduced(Approach 1). We then further modified it for our problem as discussed in Approach 2 and Approach 3.

Approach 1: Constitutive Expression

Our system is identical to the one already reported with the exception that promoter is assumed to be constitutive instead of IPTG inducible

In this approach we thereby also reproduce the results of the previously proposed model using simulations in python as follows.

The equations describing the model are given as:

Equations from original model :

Introduction to variables:

Table 2.1

N	Cell density at given point of time
Nm	Carrying capacity
k	Growth rate constant
E	Concentration of toxin
A	Concentration of AHL
kE	Production rate of toxin
dE	Degradation rate of toxin
kA	Production rate of AHL
dA	Degradation rate of AHL
d*E	Death rate of cells

The first equation is a modified logistic curve with an added death rate term (d*E*N).

The second equation describes the production of toxin(E) as linearly proportional to the AHL concentration and the third assumes that AHL(A) formed is proportional to the no of cells.

Both AHL and killer protein are assumed to degrade by first order kinetics with given rate constants.

Assuming the constitutive promoter of same strength as the IPTG inducible one there would be no change in KA .

We thus solve the ODEs for the initial condition (t=0) [N=1250 , A=0 ,E=0] .

The following values of parameters were used:

Table 2.2

Parameters for termination model (ref.1)
Parameter	Value	Unit
d	4.0E-03	nM-1h-1
dE	2	h-1
kA	4.8E-07	nM ml h-1
kE	5	h-1

Table 2.3:Two sets of values of k , NM ,dA were used in different simulations.

Table 2.3

Parameters for termination model (ref.1)
Symbol	Value for pH 6.2	Value for pH 6.6	Unit
k	0.885	0.928	h-1
NM	1.25	1.17	109 CFU/ml
dA	0.274	0.304	h-1

The results shown (in Results section) for Approach 1 are for the values of k , NM , dA given in pH 6.6 column

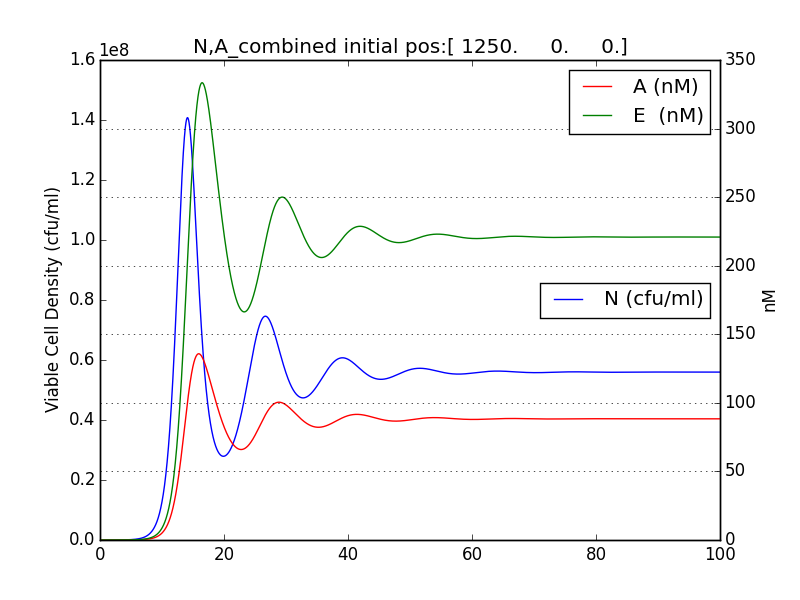
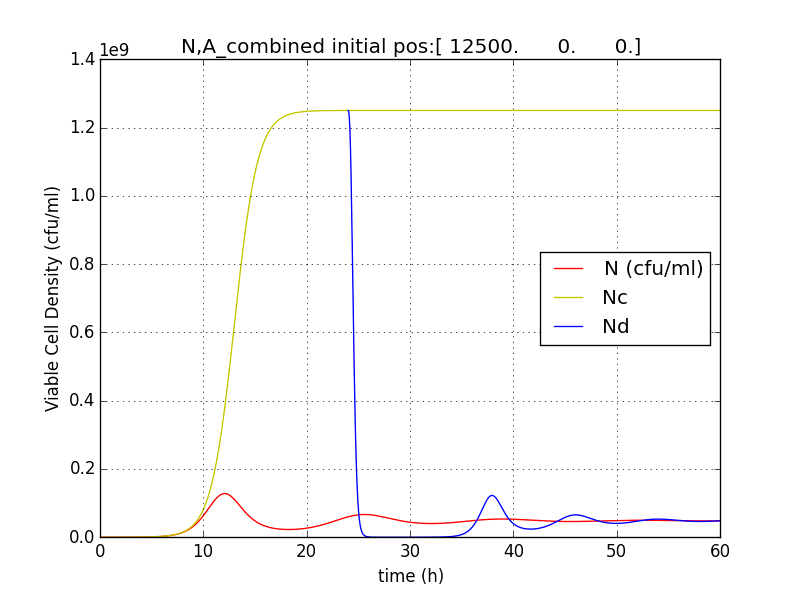
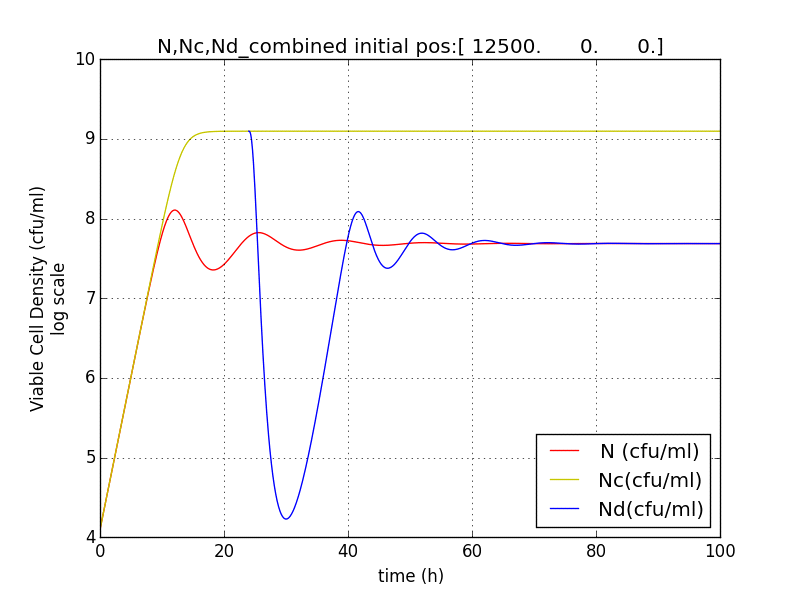
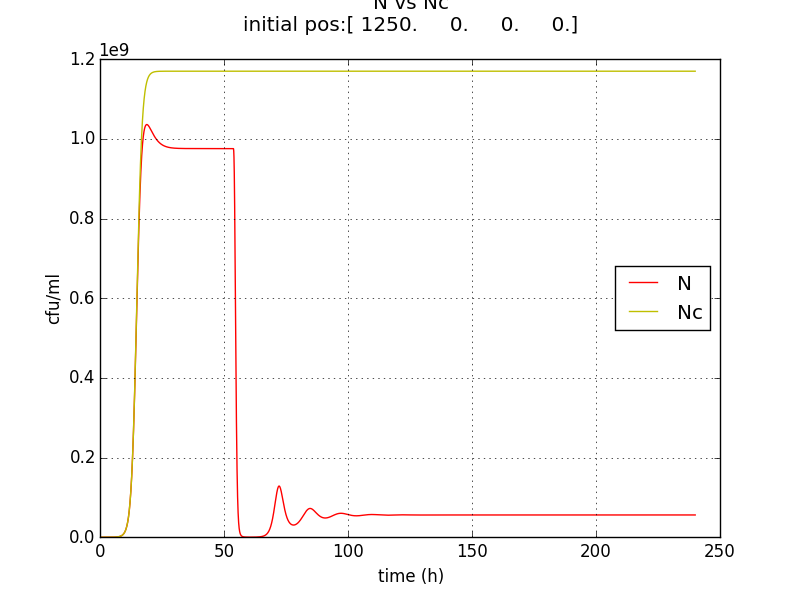
Results It was observed that terminator does not just act like a binary switch on the cell population.

The concentration of E and A also oscillate with decreasing amplitude similar to the population of cells.

Figure 2.3 Plot of N (Number of cells), A (AHL concentration), E (killer protein concentration)

Figure 2.4 Comparison with a un-induced terminator population (Nc) (predicted using logistic kinetics ) showing extent of termination.

This method/circuit of having killer gene under a constitutive/ (induced from start) does not solve our needs.

Problems:

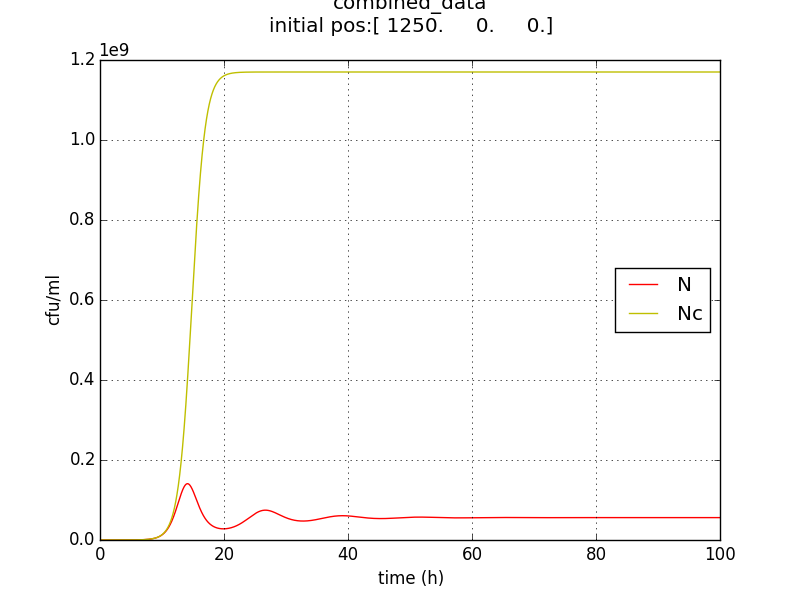
1. The population doesn’t reach a high enough population number (figure 2.4) from the beginning which unsuitable for the goal of IGEM IISER as detectability would be low.
2. N_S := stable value of N is not appreciably low. The approach doesn’t send the population to zero (or even negligible) at large t.
3. Population reduced by factor of about 20 only.

Our Work

Approach 2: Delayed termination

Based on the results of Approach 1 a delay term was introduced to allow the population to reach significant numbers initially . This was incorporated as “T” the time at which the terminator module is switched on.

T is an arbitrary time after population close to N_M is reached.

It was expected that by switching it on at a later time T(when the population is saturated) we would get better population growth initially(t<T) but since there would be more cells to terminate the post termination population would be higher (value between N_M and N_S) or it would take more time to reach the Ns population.

To mathematically simulate the scenario we broke it into two parts.

• Part 1 (t<T): Terminator circuit off.[Simple logistic curve is followed](already solved)
• Part 2 (t>T): Terminator circuit is switched on. This is same as the original problem with N_init=N_M

Merging the solutions leads to the full solution.

The same values of parameters in Table 1 used in Approach 1 are used for this simulation. The results shown are for the values of k , N_M , d_A given in pH 6.2 column in Table 2.3.

Result

Figure 2.5 Terminator is switched on at T=24h. N (population with termination from start) Nd (Population of cells after terminator switched on at t=T) Nc (Population without terminator)

Figure 2.6 Plot showing population reduction by almost 5 orders

Problems:

• The population bounces back to normal levels after a while. It doesn’t reach zero or stay low.

The problem is inherent in the model as it forces an analytic solution of Ns for the number of cells at very large times (when t tend to infinite)

Advantages

• The population falls to a numbers significantly lower (figure 2.6) than the values of the previous (constitutive) scheme for a period after terminator is triggered. This is similar to a switch like terminator we had wanted.

Therefore the delayed termination is a better strategy for termination than constitutive expression. 

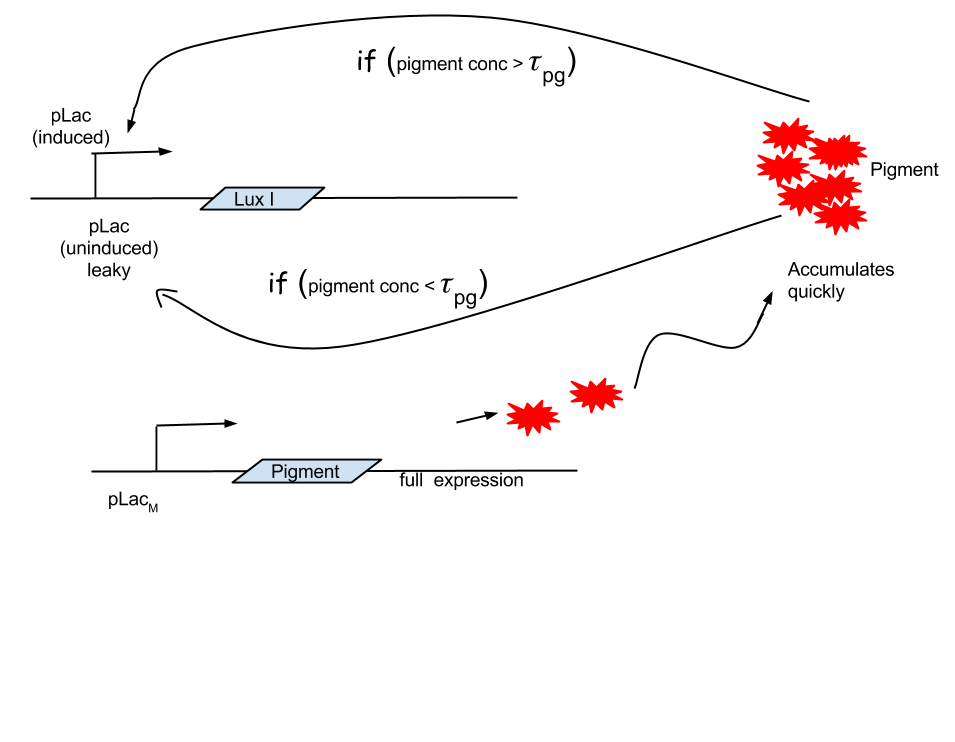
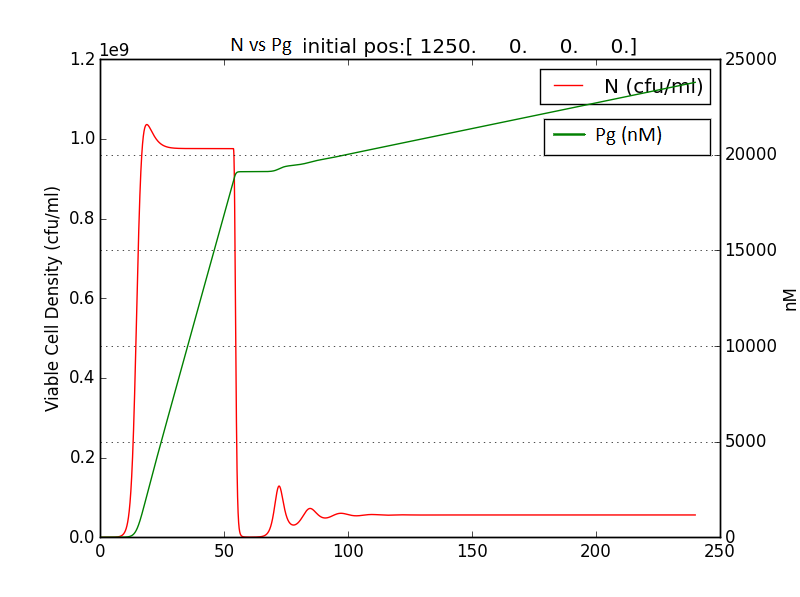
Approach 3: Pigment initiated termination

Looking at the results of Approach 2 where the delayed termination was seen to be more effective, we decided to couple it with the detection module such that the killer gene is activated when a certain concentration of pigment is reached. Our new modified module is as follows

The pigment production gene is under a constitutive promoter producing pigment from the beginning.

When certain threshold pigment concentration (τ_Pg) is achieved, the terminator is switched on.

Figure 2.2 Schematic showing pigment threshold initiated terminator

  Here our assumption is that the pigment production is proportional to number of live cells. The equation for this is:

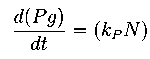
We choose to write this as: 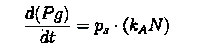where p_s is the ratio (k_P /k_A).

Since presently we do not know the rate of pigment production, for the simulation we have assumed that the pigment gene is under a promoter such that its production rate is equal to that of AHL.

To model this we keep the value p_s = 1.

The new uninduced-leaky (OFF) and fully induced (ON) states of terminator module are mathematically incorporated into our model as the follows:

Equations for our model :

When expression is leaky we assume that the production rate is proportional to k_A with proportionality constant l_A where l_A ≤ 1.

τ_Pg is the threshold concentration of pigment required for detection.

Detection:

The detection could be done by a colorimeter , computer software ,or even manual( human vision )depending on the sophistication and complexity of the setup.

We hope for our device to be accessible to a large user base.That includes even the most basic setups where access to special instruments is restricted/unavailable. So we are considering τ_Pg corresponding to visual detection. (Seeing pigment with our own eyes).

Since we hope to use lycopene as a potential indicator pigment we are choosing a value of τ_Pg parameter as the minimum concentration of lycopene required for visual identification of red color.

For this simulation τ_Pg is taken to be 1/10th the estimated concentration of lycopene in tomato juice.

Assuming the given concentration of 25.0mg/250 ml

Introduction to two extra parameters:

Table 2.3

Symbol	Parameter	Value	Units
lA	Leakiness Factor for AHL	0.01	-
τPg	Threshold Pigment Concentration	6.21E-04	M

Results

Figure 2.7 Cell population (red) against the concentration of pigment (red). Abrupt drop in number when (pigment threshold) τ_Pg reached

Figure 2.8 Comparison with a un-induced terminator population

Conclusions

The original termination model was successfully simulated in python and a method (delayed termination) was found to increase its utility for the given specific needs.

Also termination was successfully coupled to detection in a new combined model .

It can now be used to estimate the time at which termination should be activated such that pigment production and population control are optimized.

References

1. Lingchong You ,Robert Sidney Cox III, Ron Weiss & Frances H.Arnold Programmed population control by cell–cell communication and regulated killing ,Nature 428, 868-871 (22 April 2004)
2. http://www.pcrm.org/health/cancer-resources/diet-cancer/nutrition/how-lycopene-helps-protect-against-cancer

==

---

Mathematical modelling suffices to – 

Provide an objective view towards complex & apparently diverse systems. This objectivity is instrumental for efforts motivated by the idea of generalization.

Provide an ability to predict the behavior of a system i.e. to predict the properties of a state of the system given the information for some other state.

Simulations –

Give us a way in which the numbers mimic biological/chemical ‘characters’ & equations derive their behavior.

Help us in visualizing the results of equations that are analytically unsolvable.


Variable link oscillator

Description of original model from reference[1]

This is a quantitative model describing the regulation of the PRM operator region of λ phage. The model envisions that the system is a DNA plasmid consisting of the promoter region and cI gene. 
The promoter region contains the three operator sites known as OR1, OR2, and OR3. 
The gene cI expresses repressor (CI), which in turn dimerizes and binds to the DNA as a transcription factor. This binding can take place at one of the three binding sites OR1, OR2, or OR3. The binding affinities are such that, typically, binding proceeds sequentially; the dimer first binds to the OR1 site, then OR2, and lastly OR3. Positive feedback arises due to the fact that downstream transcription is enhanced by binding at OR2, while binding at OR3 represses transcription, effectively turning off production and thereby constituting a negative feedback loop. 
The chemical reactions describing the network are naturally divided into two categories – fast and slow. The fast reactions have rate constants of order seconds, and are therefore assumed to be in equilibrium with respect to the slow reactions, which are described by rates of order minutes. If we let X, X2, and D denote the repressor, repressor dimer, and DNA promoter site, respectively, then we may write the equilibrium reactions
  

where Di denotes dimer binding to the ORi site, and the Ki = ki/k−i are equilibrium constants. We let K3 = σ1K2 and K4 = σ2K2, so that σ1 and σ2 represent binding strengths relative to the dimer-OR1 strength. 
The slow irreversible reactions are transcription and degradation. If no repressor is bound to the operator region, or if a single repressor dimer is bound to OR1, transcription proceeds at a normal unenhanced rate. If, however, a repressor dimer is bound to OR2, the binding affinity of RNA polymerase to the promoter region is enhanced, leading to an amplification of transcription. Degradation is essentially due to cell growth. We write the reactions governing these processes as 
 
where P denotes the concentration of RNA polymerase, n is the number of repressor proteins per mRNA transcript, and α > 1 is the degree to which transcription is enhanced by dimer occupation of OR2. 
Defining concentrations as our dynamical variables, x = [X], x2 = [X2], d0 = [D], d1 = [D1], d2 = [D2D1], and d3 = [D3D2D1], one can write a rate equation describing the evolution of the concentration of repressor, 
 
where they assume that the concentration of RNA polymerase p0 remains constant during time. 
They next eliminate x2 and the di . The model utilizes the fact that the reactions in Eq. (1) are fast compared to expression and degradation, and write algebraic expressions 
Further, the total concentration of DNA promoter sites dT is constant, so that

 
where 
m is the copy number for the plasmid, i.e., the number of plasmids per cell.
They eliminate two of the parameters by rescaling the repressor concentration x and time. 
Now, they define the dimensionless variables x􏰄’ = x (K1K2)1/2  and t’ = t(ktp0dT n(K1K2)1/2). Upon substitution, 
 

The parameter γx is directly proportional to the protein degradation rate, and in the construction of artificial networks, it can be utilized as a tunable parameter. The integer parameter m represents the number of plasmids per cell. While this parameter is not accessible during an experiment, it is possible to design a plasmid with a given copy number, with typical values in the range of 1-100. 
The hysteretic effect can be employed to induce oscillations, provided we can couple the network to a slow subsystem that effectively drives the parameter γx. This can be done by inserting a repressor protease under the control of a separate PRM promoter region. On one plasmid, we have the network of the repressor protein CI, which is under the control of the promoter PRM , stimulates its own production at low concentrations and shuts off the promoter at high concentrations. On a second plasmid, again utilize the PRM promoter region, but here they insert the gene encoding the protein RcsA. The crucial interaction is between RcsA and CI; RcsA is a protease for repressor, effectively inactivating its ability to control the PRM promoter region.
First, both RcsA and repressor are under the control of the same promoter, so that the functional form of the production term f(x)  will be the same for both proteins. Second, they envision the network as being constructed from two plasmids – one for repressor and one for RcsA, and that we have control over the number of plasmids per cell (copy number) of each type. Lastly, the interaction of the RcsA and repressor proteins leads to the degradation of repressor. Putting these facts together, and letting y denote the concentration of RcsA, we have 
  
 We simulated this model, in python using following set of parametric values – 
 
to get –
 


 
[C1] = 7.7x + 3.0x2

We then ‘played around’ with initial conditions –

 


Inference – Initial conditions do not affect the oscillatory period, when plasmid copy number ratio is kept constant.

  The next step was to check the effect of mx : my ratio on the oscillatory system –
 
Here the ratio is kept constant – 10:1 throughout, while the values are being changed. 
Inference -  No change in the oscillatory period. However, the concentration amplitudes at which the system oscillates exhibit differences.
We then simulated the model for a range of values for mx : my ratio – 

 
Here the initial conditions are constant for all values of mx : my ratio.
Inference – For the given parametric values (referred from the paper),  the oscillatory regime is possible only for a range of plasmid copy number ratios sarting at 4:1 and giving best results (oscillations of period reuired by us) at close to 10:1.
According to our project idea, it is crucial for the entire device to be packaged in one plasmid. However, this would mean –
   
mx = my
We came up with a no. of possible mitigation strategies / alternetives for this –
1.Multiple promoter sites (i.e. gene sets)-
	Concerns : 
	Not “effective” as plasmid copy no. ratio
	Issue of promoter titration
	Larger plasmids required
2. Different RBS Efficiency ratios-
	Advantages :
	Present as bio-bricks (measurements performed)
	Efficiency ratios comparable in magnitude to copy no. ratio (from 4:1 to         10:1)
	
	
Bio-brick part	Efficiency
BBa_B0034	1.0 (Reference)
BBa_B0030	0.6
BBa_B0032	0.3
BBa_B0031	0.07
BBa_B0033	0.01

We now simulated this ‘situation’, wherein the plasmid copy number is the same for genes, but the RBS for them have different efficiencies. These RBS efficiencies are considered, if not equal, proportional to translational efficiency.
We scale  (multiply equations with appropriate factors) the equations of our oscillatory system such that –
Ratio of RBS efficiencies = Plasmid copy number ratio for which oscillations are observed.
 
RBS Efficiency Ratio 
0.6 : 0.07 = 8.75

Further work –
1.	To construct a model that includes translational & transcriptional considerations explicitly.
2.	Attempt a combinatorial way - 
	(no. of gene sets) * (RBS efficiency ratio) ≅ plasmid copy no.
	Verify the linearity!
	
	 

Terminator (Killer Gene) Model –
Description of model (from the reference)
The paper describes a circuit that programmes a bacterial population to maintain a cell density that is lower than the limits imposed by the environment (for example, by nutrient supply). This is achieved by a quorum sensing module attached to a killer gene. 
The LuxI protein of the well-characterized LuxI/LuxR system from the marine bacterium Vibrio fischeri synthesizes a small, diffusible acyl-homoserine lactone (AHL) signalling molecule. The AHL accumulates in the experimental medium and inside the cells as the cell density increases. At sufficiently high concentrations, it binds and activates the LuxR transcriptional regulator, which in turn induces the expression of a killer gene (E) under the control of a luxI promoter (pluxI). Sufficiently high levels of the killer protein (CcdB) cause cell death. The CcdB portion retains the toxicity of native CcdB, which kills susceptible cells by poisoning the DNA gyrase complex. 
A simple mathematical model is described in the reference that predicts that the system would reach a stable cell density for all realistic parameter values, although it might go through damped oscillations while approaching the steady state. 
 
They model the major kinetic events dictating the circuit function, including cell growth and death. Assumptions of the model –
 (1) without the circuit, changes in viable cell density follow logistic kinetics with an intrinsic per capita growth rate of k and a carrying capacity of Nm 
(2) for circuit-regulated growth, the cell death rate is proportional to the intracellular concentration of the killer protein (E) with a rate constant of d (h)
(3) the production rate of E is proportional to AHL concentration (A, assumed to be the same inside and outside the cells) with a rate constant of kE
(4) AHL production rate is proportional to N with a rate constant of nA 
(5) degradation of the killer protein and AHL follows first-order kinetics with rate constants of dE and dA 

  Analytical solution for this model :
 
Our work :
We simulated this model in Python, for given values of parameters & constants –
(These values were referred from the paper)
 











 

Here, 

Nc = population density when QST circuit is ‘OFF’
N = population density when QST circuit is ‘ON’

 




We also checked the behavior of A & E with respect to N.

We then came up with an idea, where we could delay the onset of terminator.
This is crucial for our device idea, as the terminator should kick in only after the system has been hijacked to extent that it produces pigment enough to be recognized visibly.
# add schematic

Hence, we coupled our detection module with the terminator module. Depending on the whether the concentration of pigment has crossed a threshold value, the killer gene is activated.

Pigment production gene under a constitutive promoter, accumulates continuously. When sufficient (visible to eye, here assumed to be 1/10 conc. of that of lycopene in tomato) amount of pigment is accumulated, the sender (AHL producing part of the circuit) of the terminator is induced, which then in turn induces the killer gene in the receiver.
This pigment- sender induction can either be manual (as this model now helps us to know the time period in which ‘sufficient’ amount of pigment accumulates) or through a density counter associated with the pigment production gene.
   

 

N= QST on
Nc=QST off
Nd=Delayed initiation

References :
1)	Designer gene networks towards funamnetal cellular control, Hasty et al, Chaos (2002)
2)	Programmed population control by cell-cell communication and regulated killing, You et al, Nature (2004)