Team:ETH Zurich/Modeling/Reaction-diffusion
- Project
- Modeling
- Lab
- Human
Practices - Parts
- About Us
Reaction-diffusion Models
Introduction
One of the two signals used by our CTC detection system is the detection of apoptotic cancer cells through quorum sensing between E. coli cells colocalized around them. However, for this to be a useful signal as part of an AND gate, E. coli within the same experimental environment (in our case, a well) as a mammalian cell must only trigger the loop if they are colocalized and the cell produces a high amount of lactate, or at least trigger after a sufficient amount of time. By accurately simulating the diffusion of the two chemical species AHL and lactate through the environment, the efficacy of our quorum sensing module as a signal of colocalization can be assessed.
The results from these simulations show that due to the small size of the well in which the experiment takes place, the generation of a slightly higher AHL concentration around the mammalian cell is only possible due to the strong binding of LuxR to AHL. Unbound AHL diffuses through a 1 nL well in about 6 minutes, thus quickly diminishing its concentration gradient. However, the greater capture of lactate by cells bound to the target cell relative to free-floating cells creates a concentration gradient of LuxR which translates to a difference in GFP signal between bound and unbound cells. Combinatorially testing cases where E. coli cells bind or float around high- or low-rate lactate producers shows that our system acts as an AND gate of the two cancer markers, with E. coli bound to a high lactate producer fluorescing at a greater strength and the other cases exhibiting intermediate levels of fluorescence.
Goals
We need to use a reaction-diffusion model to fully understand the flow of the intercellular chemical species, and hence, our system's functionality. Through this modeling, we aim to explore
- the diffusion of AHL and lactate through the well
- the self-activation time of the system in different well volumes
- the relative capture of secreted lactate by bound and unbound E. coli
- the influence of logistic growth of the E. coli on the activation time
- simulation of the system in a water droplet suspended in an oil flow
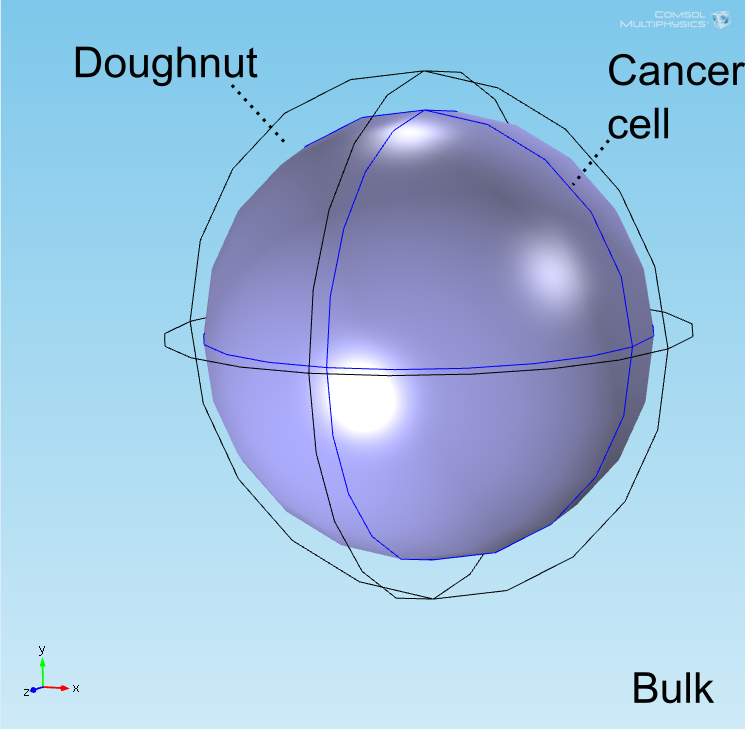
The "doughnut" model
Introduction
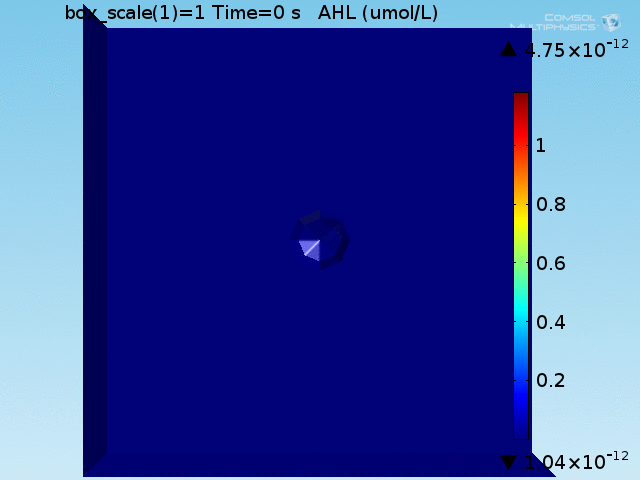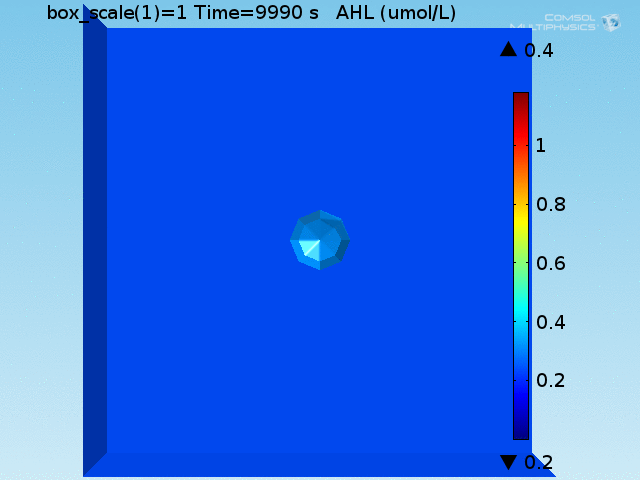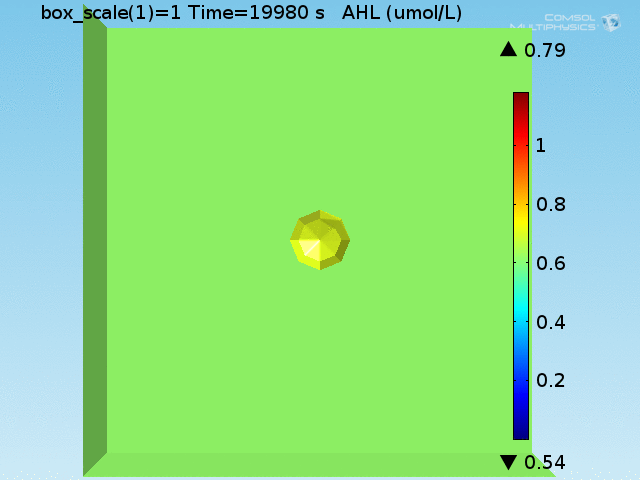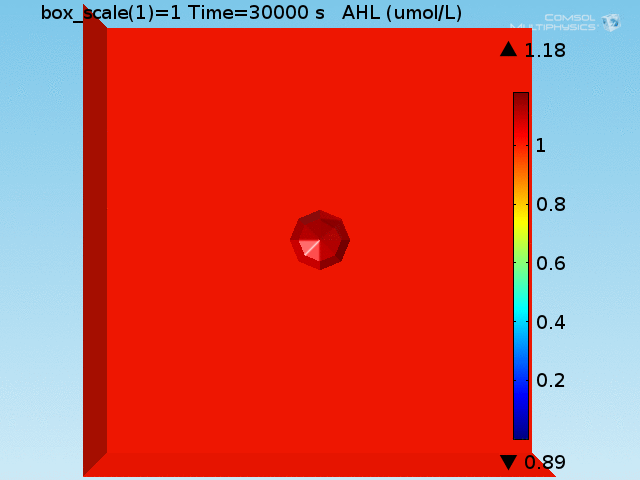
After implementing the single-cell models in the COMSOL multiphysics software package in an analogous geometry as a control, a more accurate geometry was constructed. Preliminary simulations were done in a geometry where a central circle representing the target cell was surrounded with smaller circles representing bound E. coli and circles uniformly distributed in the remaining space represented unbound E. coli. It was quickly realized, however, that this would not be an accurate representation of our test due to the rapid growth of the E. coli population. To address this, the discrete circles were abstracted to connected spaces representing the union of a collection of cells to allow for population growth to be simulated by modification of the ODE system over time. Owing to the shape of the layer of E. coli bound to the target cell, this geometry is referred to as the "doughnut" model. The AHL and lactate modules were implemented and tested separately before being combined into a full model.
All mathematical derivations are done in general, with values for variables being defined in the definition of our model geometry and assumptions, and in the parameters page.
Abstraction of discrete E. coli to a connected space
The well in which our reaction takes place is a box of length 100μm. In the middle of the well, we have a circle representing our target cell surrounded by a ring (called the doughnut) of width equal to the diameter of an E. coli cell representing the union of all bound E. coli cells (see Figure 1). Finally, the remaining space represents both the medium and free-floating E. coli cells, which we refer to as the bulk. All species are able to diffuse freely through this medium and rates for our reactions are adjusted based on the size of the E. coli population at a given time.
Assumptions
- One non-dividing target cell per well
- Uniform distribution of cells in their respective spaces
- A cell unbinding from the target is immediately replaced, so cell density in the doughnut is constant and maximal
- Logistic growth of E. coli in the bulk with a doubling time of 30 minutes
- E. coli take up lactate, but do not export it

Lactate Module
Lactate uptake by cells
The simulations performed to characterize the lactate module make assumptions that are too stringent in the context of our testing environment. High rates of lactate production by the cancer cell do not readily translate to equivalent intracellular concentrations in the E. coli cells. In particular, those cells within the doughnut domain will capture a greater fraction of the excreted lactate due to its higher apparent concentration immediately around the target cell. Therefore, a simulation of the diffusion of lactate through the well and its capture by E. coli will provide a better idea of the input for our sensor. Due to the dilution of lactate caused by the its entry into the bulk and for computational simplicity, it is assumed that all lactate entering the bulk is taken up by the bulk E. coli.
The uptake and excretion rates set for lactate lead to a 20:1 ratio of lactate concentration between the doughnut and the bulk, as described in the literature. Of the 700 μM of lactate produced by the target cells,
AHL Module
Diffusion of AHL and self-activation time with logistic population growth
One of the assumptions made in the AHL module to test worst-case behavior was that the bulk is maximally populated with E. coli. More accurately, we can model the growth of an initial population in the bulk. Suppose we start with an initial E. coli population corresponding to an optical density of \(OD_{600}=0.1\) and a carrying capacity corresponding to \(OD_{600}=2\), with a doubling time of 30 minutes.
Nanoliter well with constant velocity flow
Although the original testing environment of water droplets suspended in a flow of oil could not be put into practice due to time constraints, a simulation of this setup was done to predict how it would have affected our results. Having a constant velocity flow in a channel with an open boundary with the well is equivalent to increasing the well's volume, thus, should result in similar effects. However, the apparent volume of the system may become so large that the system never triggers regardless of lactate input.
When a laminar flow with an open boundary

Initial model: Diffusion of AHL and self-activation time with constant population
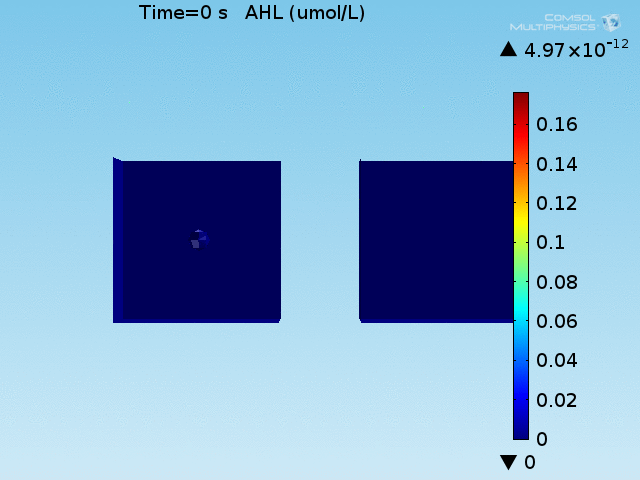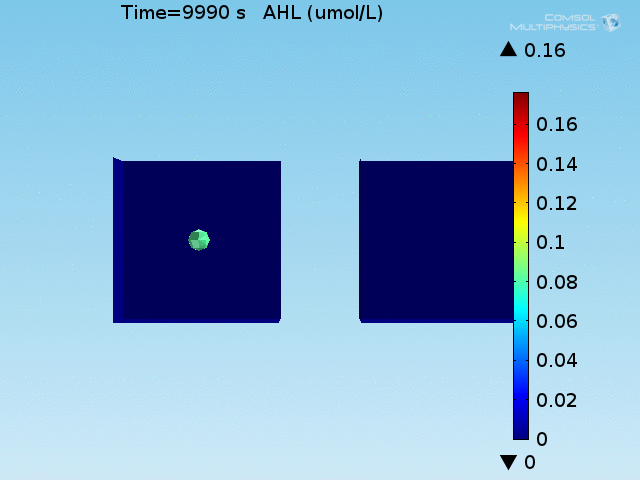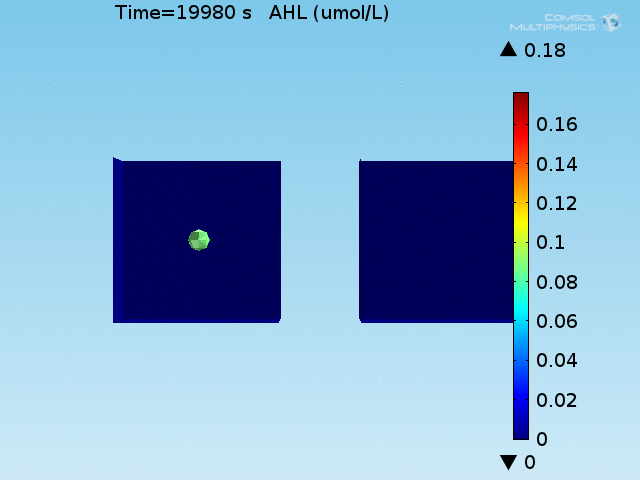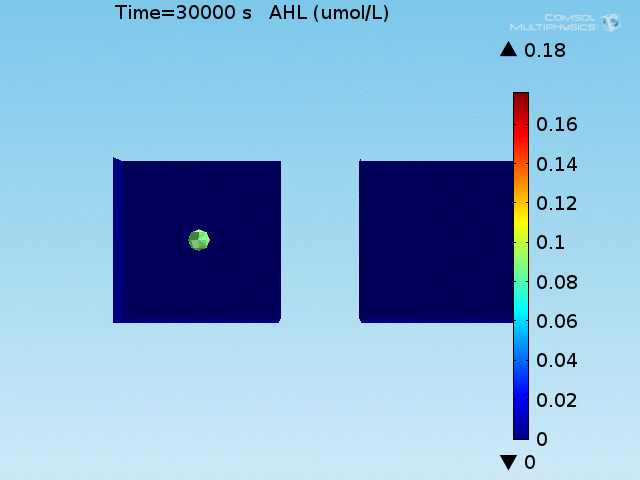
For these simulations, it was assumed that all cells contain a constant amount of LuxR corresponding to the maximal concentration determined by the lactate module to study the effects of cell colocalization. Despite the orders-of-magnitude difference in the diffusion coefficients of AHL through water and across cell membranes, it is apparent that on a time scale of minutes, AHL is able to diffuse across the entire well. The small difference in concentrations between the wells with binding cells and floating wells can be attributed to a ~10% difference in total cell counts between these wells.
In wells of volumes 1 nL, 10 nL, and 100 nL, the AHL concentration reaches a sufficient concentration to activate the system in 10 minutes, x minutes, and y minutes, respectively. Thus, a 100 nL well is sufficient to differentiate the two cases on our experimental timescale.

Full Model
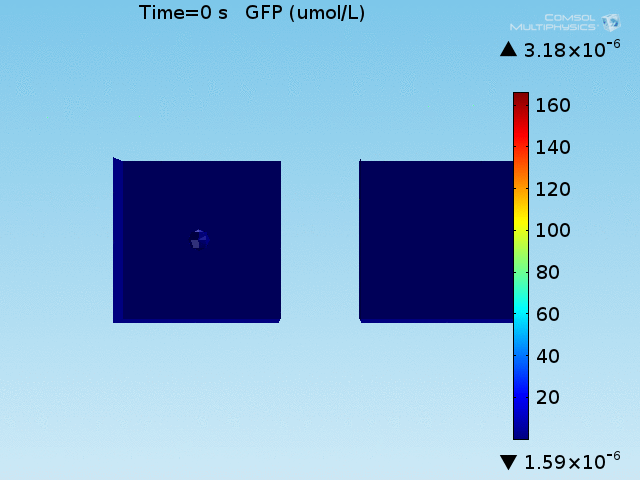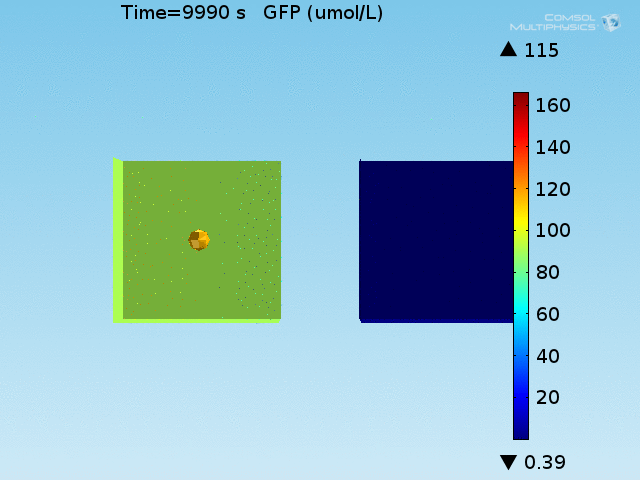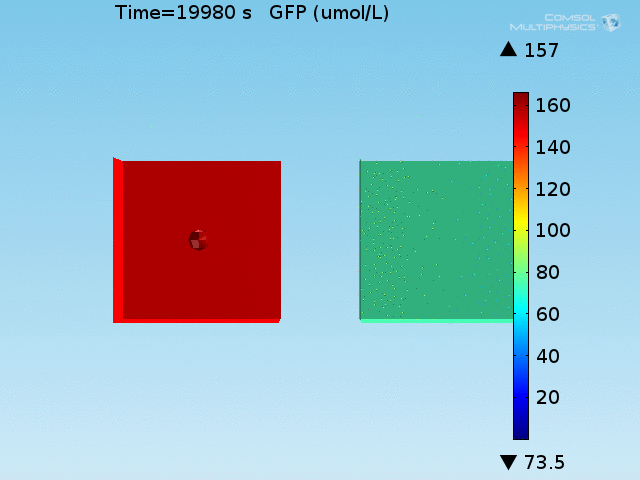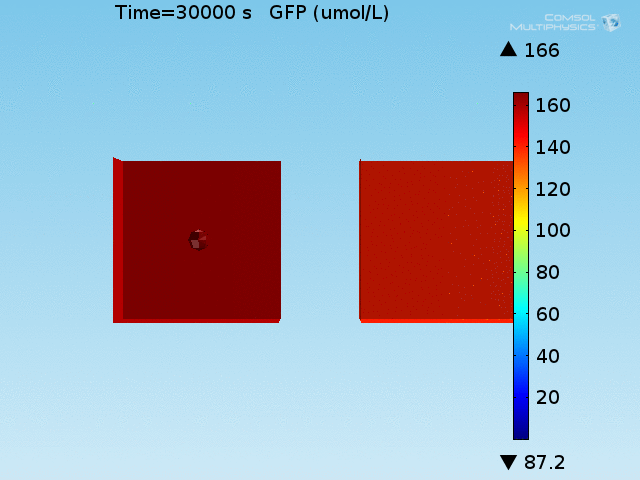
An AND-gate of the signals
When the lactate and AHL modules are combined, including the effects of AHL and lactate diffusion, lactate capture, and E. coli population growth, the response of the system on its two inputs in this more accurate model can be assessed. Rather than representing the two inputs as continuous variables as shown in the compartment model, they are represented in four discrete states
- High lactate production rate (cancer cell), doughnut of bound bacteria (ON-ON)
- High lactate production rate, no binding of bacteria (ON-OFF)
- Normal lactate production rate (normal cell), doughnut of bound bacteria (OFF-ON)
- Normal lactate production rate, no binding of bacteria (OFF-OFF)
From figures x and y, it is clear that the environment in which both signals are present triggers the system, whereas a delayed and lower-amplitude response is produced by the system in which the bacteria colocalize around a normal cell. Consistent with the results from the compartment model, the OFF-ON trial is an intermediate between the ON-ON and OFF-OFF states.
Concentrations detected by microscopy
All modeling results previously have reported the concentrations of the chemical species within a single cell in its respective environment, either in the doughnut or the bulk. However, when our detection system is implemented in a chip, the total concentration of GFP within a domain will be measured and not the per-cell concentration. This dilution effect of the apparent concentration means that reported concentrations in the bulk will differ from what has been simulated due to the low density of cells in the bulk.
When the concentration of GFP is corrected for this dilution effect, the signal ratio between the two domains is much greater.
- A) Error creating thumbnail: File missing
- B) Error creating thumbnail: File missing
Figure b: Ratios of GFP concentration between the ON-ON trial and all others. A) Per-cell ratios B) Microscopy concentration ratios.
Simulation of a flow
Although a difference in signal is produced by
- Error creating thumbnail: File missing
- Error creating thumbnail: File missing
- Error creating thumbnail: File missing
Figure z: GFP, captured lactate, and LuxR concentrations of a single cell when an environment with a water droplet suspended in oil is simulated.

Summary
By modeling the diffusion of lactate through our well, we have demonstrated that the E. coli bound to their target cell, through active transport and capture by binding to LldR, reduce the accessible lactate concentration of the unbound cells, producing a concentration gradient of its output signal LuxR.
Simulations of the AHL module demonstrated that the leakiness of the LuxR promoter leads to the self-activation of this module within our experiment's timeframe. The degradation of AHL via the action of AiiA did not lead to a drastic change in this behavior, while the introduction of riboregulation to the LuxR promoter tied to LuxI suppressed self-activation sufficiently.
One major feature of the system that could not be implemented fully due to time constraints was the binding and unbinding of E. coli to the target cell. All models have assumed that this binding has already happened and that a cell that has bound does not unbind.
Model Details
Logistic growth of E. coli
Let us define \(n_\text{bulk}:[0,t_\text{sim}]\longrightarrow \mathbb N\) as the function representing the size of the E. coli population in the bulk at time \(t\), with an initial population size of \(n_0\), a carrying capacity of \(K\), and a growth rate of \(R\). The closed-form equation of this function is then $$n_\text{bulk}(t) = \frac{n_0 K e^{Rt}}{K + n_0(e^{Rt}-1)}$$
If we denote the doubling time of the population by \(t_2\), we can solve for the growth rate \(R\) and define a new constant \(g\) s.t. $$R = \frac{\log2 + \log(K+n_0) - \log(K-2n_0)}{t_2} =: \frac{\log g}{t_2}$$ When we plug this value back into the original equation, it simplifies to $$n_\text{bulk}(t) = \frac{n_0 K g^{\frac{t}{t_2}}}{K + n_0(g^{\frac{t}{t_2}}-1)}$$ Finally, if we define the time we end our experiment, denoted \(t_\text{sim}\), as the time when the population reaches size \((1-\varepsilon)K\) for some small \(\varepsilon>0\), then we can solve for \(t_\text{sim}\) $$t_\text{sim} = \frac{1}{R}\log\frac{(K-n_0)(1-\varepsilon)}{n_0\varepsilon}$$
Carrying capacity
Some stuff here about the carrying capacity.

Diffusion and transport of chemical species
Under alkaline conditions, E. coli actively import lactate via a proton-motive symporter lldP.[] Thus, a cross-membrane transport reaction had to be implemented. Since diffusion across barriers is implemented with equal diffusion coefficients for both directions in COMSOL, the transport of lactate across the doughnut membrane was implemented by modeling two different states of unbound lactate. If we let our reference space be the interior of the doughnut, we can define two pseudo-species \(Lact_\text{in}\) and \(Lact_\text{out}\), denoting intracellular and extracellular lactate, respectively. \(Lact_\text{out}\) is produced by the target cell and can diffuse freely though the medium and all membranes, while \(Lact_\text{in}\) is converted irreversibly from \(Lact_\text{out}\) and cannot diffuse out. $$ Lact_\text{out} \mathop{\mathop{\xrightarrow{\hspace{4em}}}^{\xleftarrow{\hspace{4em}}}}^{k_{\mathrm{ext}}}_{k_\text{int}} Lact_\text{in} $$ Only the \(Lact_\text{in}\) state can react with the other chemical species in the doughnut and only \(Lact_\text{out}\) can react with other chemical species in the bulk. The value of \(k_\text{ext}\) was estimated based on (REF), while \(k_\text{int}\) was set to maintain a \(k_\text{ext}:k_\text{int}\) ratio of 20.
Since AHL can freely diffuse across membranes, unbound AHL is only modeled as one state that can diffuse across all barriers. The effective diffusion coefficient of lactate was estimated relative its coefficient in water \(D_{aq}\) by the relation $$\frac{D_e}{D_{aq}}\approx 0.25$$ using the approximation proposed in a 2003 review by Stewart. The diffusion coefficient of AHL through the membrane was computed from an AHL excretion rate of \(D_m = 100 \text{min}^{-1}\) REF.
Correcting concentrations
Since E. coli are not fully packed into the domains in our model, a concentration correction has to be applied to the chemical species. If no correction is made for the strictly intracellular species, then the reported concentrations are single-cell. To compensate for the fact that AHL can diffuse across membranes, its production rate is scaled by the ratio of the total E. coli volume and the volume of the domain they are present in. Although this relation assumes instant diffusion of AHL, the small volume of the well makes this assumption approximately hold on our simulation timescale.
Flow
Since it is assumed that the presence of a constant flow of fluid on the top boundary of a well will draw away all of the free-floating molecules, this was implemented as a 0-concentration boundary condition on the top of the well.
Simulation in COMSOL Multiphysics
All simulations were run with 1000 time steps and a course mesh. For the full model, the course mesh led to convergence issues in the nonlinear solver, so a normal mesh was used.