Difference between revisions of "Team:Uniandes Colombia/DryLab"

 
(7 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
<html>
 
<html>
 
<h1> Mathematical Models </h1>
 
<h1> Mathematical Models </h1>
−
$$ \forall \alpha$$
+
<br><br>
−
<p> We use a mathematical model to check if the design works before starting to work at the laboratory, or improve the response of the original construct. To develop this model the first step is to create a deterministic model, which is based on differential equations. This type of model describes the mean behavior for each of the substances in the synthetic circuit over time. However, it does not take into account the probabilities involved in each of the events described, the population interactions and the noise of the system.</p>
+
<p> We use a mathematical model to check if the design works before starting to work at the laboratory, or improve the response of the original construct. To develop this model, the first step was to create a deterministic model, which was based on differential equations. This type of model describes the mean behavior for each of the substances in the synthetic circuit over time. However, it does not take into account the probabilities involved in each of the events described, the population interactions or the noise of the system.</p>
 
<p>The deterministic model is based on the law of mass conservation and expresses the inputs and outputs of the system with expressions that use the law of mass action and known models like Hill's or Michaelis Menten.However, we only have a model that shows a response that does not take into account the stochasticity of Nature. That's why did a second simulation: The stochastic Model. You are very welcome to check it all.</p>
 
<p>The deterministic model is based on the law of mass conservation and expresses the inputs and outputs of the system with expressions that use the law of mass action and known models like Hill's or Michaelis Menten.However, we only have a model that shows a response that does not take into account the stochasticity of Nature. That's why did a second simulation: The stochastic Model. You are very welcome to check it all.</p>
 
<br><br><br><br>
 
<br><br><br><br>
 
<div class="highlightBox"  style="text-align:center">
 
<div class="highlightBox"  style="text-align:center">
 
<h2> Differential equations </h2>
 
<h2> Differential equations </h2>
 +
<br><br>
 +
<h3>Synechococcus elongatus </h3>
 +
<br><br>
 +
<p>Our clock protein binds to our promoter(pCL) and then transcribes LuxI and LacI proteins. We have to take into account the degradation(g) and the diffusion coefficient(c) if it is needed.  After that, the two proteins go through independent paths. </p>
 +
<br><br>
 +
<p><b>Lux I Equation
 +
</b></p>
 +
<p>LuxI has a basal production (alpha), a degradation rate (gamma), and is positively regulated by the clock protein. This positive regulation is represented as a hill equation for activated genes, represented through the second term.</p>
 +
 
$$ \frac{dXI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{XI}*XI$$
 
$$ \frac{dXI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{XI}*XI$$
 +
<p>The product of luxI catalyzes the production of AHL
 +
</p>
 +
<br><br>
 +
<p><b>Lac I Equation</b></p>
 +
<p>The terms that describe la I are analogous to those of luxI. There is a basal production rate (alpha), a degradation rate (gamma), and a term describing lacI production due to positive regulation by the clock protein (hill equation for genes that are positively regulated).
 +
</p>
 +
 
$$ \frac{dLI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{LI}*LI$$
 
$$ \frac{dLI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{LI}*LI$$
 +
 +
<br><br>
 +
<p><b>Intracellular AHL-degrading enzyme equation </b></p>
 +
<p>This enzyme, encoded by the aaiA gene, has a basal production (alpha), a degradation rate (gamma), a term accounting for how the negative feedback due to lacI (hill equation for genes with a negative regulator) influences the enzyme production, and a negative term  (c) due to difussion outside the cell.
 +
</p>
 +
<br><br>
 +
 
$$ \frac{dEA_{i}}{dt}=a_{L}+\frac{b_{s}}{1+(\frac{LI}{k_{L}})^{n_{L}}}-g_{LI}*LI$$
 
$$ \frac{dEA_{i}}{dt}=a_{L}+\frac{b_{s}}{1+(\frac{LI}{k_{L}})^{n_{L}}}-g_{LI}*LI$$
−
<p> Shewanella </p>
+
<br><br>
 +
<h3> Shewanella </h3>
 +
<br><br>
 +
<p><b>LuxR </b></p>
 +
<p>LuxR has a basal production (alpha), a degradation rate (gamma), a negative term due to its coupling to AHL, and a positive term due to its decoupling from AHL.
 +
</p>
 +
<br><br>
 
$$\frac{dXR}{dt}=a-b_{XR}*XR*A-g_{XR}*XR+d_{XRa}*XRa$$
 
$$\frac{dXR}{dt}=a-b_{XR}*XR*A-g_{XR}*XR+d_{XRa}*XRa$$
 +
<br><br>
 +
<p><b>LuxR-AHL complex</b></p>
 +
<p>The formation of the complex depends on a formation rate (ba) and the concentrations of LuxR (XR) and AHL (A). It also has a degradation rate  (gamma), and a negative term due to decoupling of the complex (at a rate dXR).
 +
</p>
 +
<br><br>
 
$$\frac{dXRa}{dt}=b_{XR}*XR*A-g_{XRa}*XRa+d_{XR}*XRa$$
 
$$\frac{dXRa}{dt}=b_{XR}*XR*A-g_{XRa}*XRa+d_{XR}*XRa$$
 +
<br><br>
 +
<p><b>Cytochrome Equation</b></p>
 +
<p>Cytochromes have a basal production (alpha), a degradation rate (gamma), and a production due to the attachment of the LuxR-AHL complex to the promoter. </p>
 +
<br><br>
 
$$\frac{dCY}{dt}=a_{X}+k_{c}*XR*A-g_{CY}*XR$$
 
$$\frac{dCY}{dt}=a_{X}+k_{c}*XR*A-g_{CY}*XR$$
 +
<br><br>
 
</div>
 
</div>
  
 +
<div class="highlightBox"  style="text-align:center">
 +
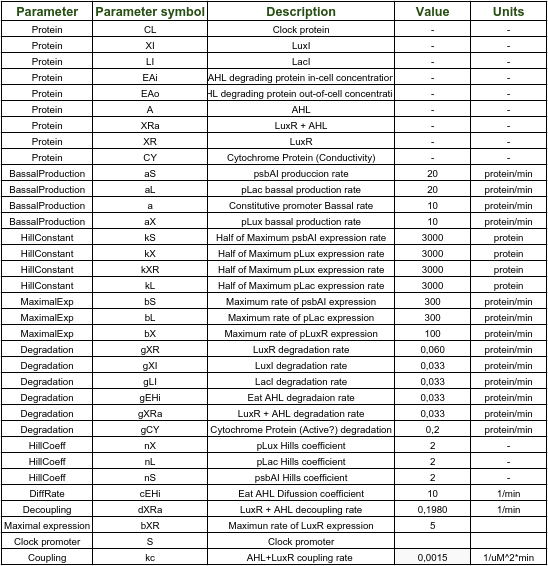
<h2> Parameters </h2>
 +
<br><br>
 +
<p>The parameters used in our simulation can be found in the table below:</p>
 +
 +
<br><br>
 +
 +
</html>[[File:Tablaparcol.png]]<html>
 +
<br><br>
 +
</div>
  
 
<div class="highlightBox"  style="text-align:center">
 
<div class="highlightBox"  style="text-align:center">
 
<h2> Deterministic model </h2>
 
<h2> Deterministic model </h2>
 +
<br><br>
 +
<p>Pclock varies sinusoidally with time. That's why a sinusoidal input was given for it.</p>
 +
<br><br>
 +
<h3>Synechococcus elongatus </h3>
 +
<br><br>
 +
</html>[[File:Cyanodet.png]]<html>
 +
<br><br>
 +
<p>As evidenced in the graph above, AHL also behaves sinusoidally as an output. Consequently, it is logical to have a sine wave with a 24hr period as input for Shewanella oneidensis</p>
 +
<br><br>
 +
<h3>Shewanella oneidensis</h3>
 +
<br><br>
 
</html>[[File:Shdef.png]]<html>
 
</html>[[File:Shdef.png]]<html>
 +
<br><br>
 +
<p>It was thus shown that with the given parameters, the cytochromes (and so the resistance) in Shewanella</p>
 +
 
</div>
 
</div>
 
<div class="highlightBox"  style="text-align:center">
 
<div class="highlightBox"  style="text-align:center">
Line 60: Line 123:
  
 
<p>The following graphs display the outcome of the simulations for Synechococcus elongatus and Shewanella oneidensis. </p>
 
<p>The following graphs display the outcome of the simulations for Synechococcus elongatus and Shewanella oneidensis. </p>
 +
<br><br>
  
−
<h1> <i>Synechococcus elongatus </i> </h1>
+
<h4> <i>Synechococcus elongatus </i> </h4>
−
</html>[[File:ShewanellaestocasbX40.png]]<html>
+
−
<center><b> Figure 1 </b></center>
+
−
<h1> <i>Shewanella oneidensis </i> </h1>
+
 
</html>[[File:Cyano.png]]<html>
 
</html>[[File:Cyano.png]]<html>
−
<center><b> Figure 2 </b></center>
+
<center><b> Figure 1 </b></center>
 +
<br><br>
  
 +
 +
<h4> <i>Shewanella oneidensis </i> </h4>
 +
</html>[[File:ShewanellaestocasbX40.png]]<html>
 +
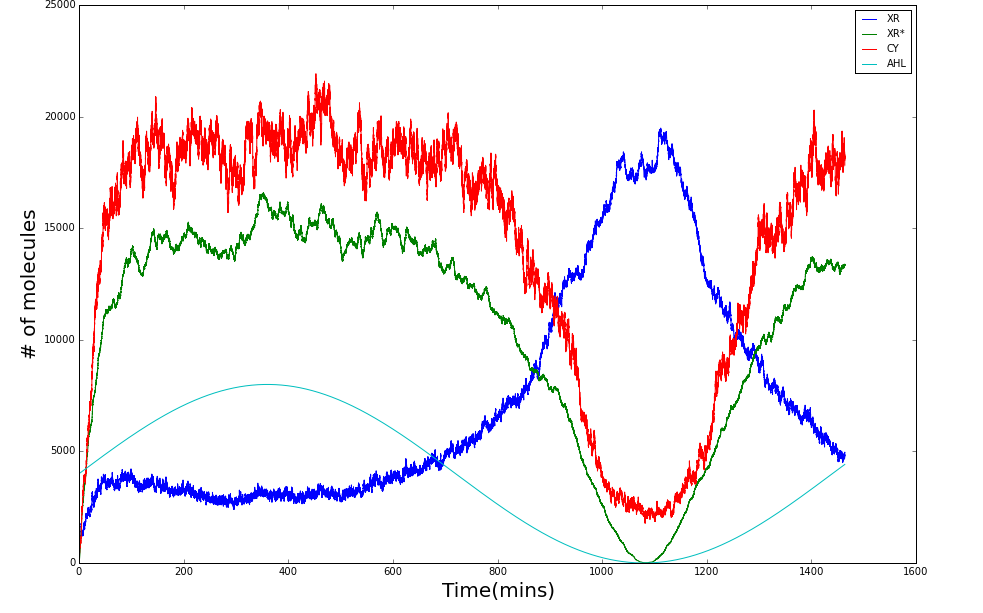
<center><b> Figure 2 </b></center>
 +
<br><br>
 
</div>
 
</div>
  
 +
<div class="highlightBox"  style="text-align:center">
 +
<h2> Scripting </h2>
 +
<br><br>
 +
<h3> Deterministic Model </h3>
 +
<br><br>
 +
<p>Synechococcus elongatus</p>
 +
<textarea readonly rows = "20">
 +
 +
%pylab inline
 +
#we define first the value of h and the corresponding range in x
 +
h=0.2
 +
n_points = int((4000.0)/h)
 +
t = zeros(n_points)
 +
XI = zeros(n_points)
 +
LI = zeros(n_points)
 +
EA = zeros(n_points)
 +
CL = zeros(n_points)
 +
gLI=0.0231
 +
size(CL)
 +
#definimos todas las ecuaciones
 +
def func_XI_prime(t,XI,LI,EA,CL):
 +
    return 0+((400*pow(CL,2))/(pow(CL,2)+pow(3000,2)))-(1/30.0)*XI
 +
def func_LI_prime(t,XI,LI,EA,CL):
 +
    return 5+((300*pow(CL,2))/(pow(CL,2)+pow(4000,2)))-(gLI)*LI
 +
def func_EA_prime(t,XI,LI,EA,CL):
 +
    return 1+((300)/(1.0+(pow(LI,2)/pow(4000,2))))-(1/30.0)*EA
 +
 +
 +
t[0] = 0.0
 +
XI[0] = 0.0
 +
LI[0] = 0.0
 +
EA[0] = 0.0
 +
CL[0] = 0.0
 +
 +
for i in range(1400):
 +
    CL[i]=0.0
 +
for i in range(1401,n_points):
 +
    CL[i]=4000*sin(t[i]/300)+4000
 +
 +
   
 +
for i in range(1,n_points):
 +
 
 +
    k1_XI = func_XI_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1])
 +
    k1_LI = func_LI_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1])
 +
    k1_EA = func_EA_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1])
 +
 +
    #first step
 +
    t1 = t[i-1] + (h/2.0)
 +
    XI1 = XI[i-1] + (h/2.0) * k1_XI
 +
    LI1 = LI[i-1] + (h/2.0) * k1_LI
 +
    EA1 = EA[i-1] + (h/2.0) * k1_EA
 +
 +
    k2_XI = func_XI_prime(t1,XI1,LI1,EA1,CL[i-1])
 +
    k2_LI = func_LI_prime(t1,XI1,LI1,EA1,CL[i-1])
 +
    k2_EA = func_EA_prime(t1,XI1,LI1,EA1,CL[i-1])
 +
 +
 +
    #second step
 +
    t2 = t[i-1] + (h/2.0)
 +
    XI2 = XI[i-1] + (h/2.0) * k2_XI
 +
    LI2 = LI[i-1] + (h/2.0) * k2_LI
 +
    EA2 = EA[i-1] + (h/2.0) * k2_EA
 +
   
 +
    k3_XI = func_XI_prime(t2,XI2,LI2,EA2,CL[i-1])
 +
    k3_LI = func_LI_prime(t2,XI2,LI2,EA2,CL[i-1])
 +
    k3_EA = func_EA_prime(t2,XI2,LI2,EA2,CL[i-1])
 +
       
 +
    #third step
 +
    t3 = t[i-1] + h
 +
    XI3 = XI[i-1] + (h/2.0) * k3_XI
 +
    LI3 = LI[i-1] + (h/2.0) * k3_LI
 +
    EA3 = EA[i-1] + (h/2.0) * k3_EA
 +
   
 +
    k4_XI = func_XI_prime(t3,XI3,LI3,EA3,CL[i-1])
 +
    k4_LI = func_LI_prime(t3,XI3,LI3,EA3,CL[i-1])
 +
    k4_EA = func_EA_prime(t3,XI3,LI3,EA3,CL[i-1])
 +
   
 +
    #fourth step
 +
    average_k_XI = (1.0/6.0)*(k1_XI + 2.0*k2_XI + 2.0*k3_XI + k4_XI)
 +
    average_k_LI = (1.0/6.0)*(k1_LI + 2.0*k2_LI + 2.0*k3_LI + k4_LI)
 +
    average_k_EA = (1.0/6.0)*(k1_EA + 2.0*k2_EA + 2.0*k3_EA + k4_EA)
 +
 +
    t[i] = t[i-1] + h
 +
    XI[i] = XI[i-1] + h * average_k_XI
 +
    LI[i] = LI[i-1] + h * average_k_LI
 +
    EA[i] = EA[i-1] + h * average_k_EA
 +
   
 +
    if (i < 1400):
 +
        CL[i]=0.0
 +
    if (1401<i<n_points):
 +
        CL[i]=4000*sin(t[i]/300)+4000
 +
 +
   
 +
plot(t,XI,label='XI')
 +
#plot(t,LI,label='LI')
 +
plot(t,EA,label='EA')
 +
plot(t,CL,label='CL')
 +
plt.xlabel('t(min)',size=20)
 +
plt.ylabel('proteins',size=20)
 +
legend()
 +
figure(figsize(15,10))
 +
plt.savefig("Cyanodet.png", format='png')
 +
 +
</textarea>
 +
 +
<br><br>
 +
<p>Shewanella onediensis</p>
 +
 +
<textarea readonly rows = "20">
 +
%pylab inline
 +
#First,we define the value of h,the corresponding range in x and the constants
 +
#If you need more information about the parameters of our model please visit our Wiki.
 +
h=0.2 #step value
 +
a=10.0
 +
bXR=5.0
 +
kXR=3000.0
 +
gXR=0.06
 +
dXRa=0.1980 #actived XR
 +
aX=10.0
 +
bX=100.0
 +
kc=0.0015
 +
nX=2.0
 +
kx=10000.0
 +
gCY=0.25
 +
kXRa=3000.0
 +
gXRa=0.0231
 +
dXR=10.0
 +
 +
n_points = int((4000.0)/h)
 +
#Here we create the the arrays that represent the variables in the differential equations.
 +
t = zeros(n_points)
 +
XR = zeros(n_points)
 +
CY = zeros(n_points)
 +
XRa = zeros(n_points)
 +
A = zeros(n_points)
 +
 +
 +
#we define all the functions
 +
 +
def func_XR_prime(t,XR,CY,XRa,A):
 +
    return a +((bXR)/(1.0+(A/kXR)))-(gXR*XR)+(dXRa*XRa)
 +
 +
def func_CY_prime(t,XR,CY,XRa,A):
 +
    return aX+(kc*A*XR)-(gCY*CY)
 +
 +
def func_XRa_prime(t,XR,CY,XRa,A):
 +
    return (bXR/(1.0+(A/kXR)))-(gXRa*XRa)-(dXRa*XRa)
 +
#First we initialize the arrays
 +
t[0] = 0.0
 +
XR[0] = 0.0
 +
CY[0] = 0.0
 +
XRa[0] = 0.0
 +
A[0] = 0.0
 +
#then we determine the input function
 +
for i in range(1400):
 +
    A[i]=0.0
 +
for i in range(1401,n_points):
 +
    A[i]=4000*sin(t[i]/200)+4000
 +
   
 +
   
 +
#And finally we do 4th order Runge Kutta.
 +
for i in range(1,n_points):
 +
   
 +
    if (i < 1400):
 +
        A[i]=0.0
 +
    if (1401<i<n_points):
 +
        A[i]=4000*sin(t[i]/200)+4000
 +
 
 +
    k1_XR = func_XR_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1])
 +
    k1_CY = func_CY_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1])
 +
    k1_XRa = func_XRa_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1])
 +
   
 +
   
 +
    #first step
 +
    t1 = t[i-1] + (h/2.0)
 +
    XR1 = XR[i-1] + (h/2.0) * k1_XR
 +
    CY1 = CY[i-1] + (h/2.0) * k1_CY
 +
    XRa1 = XRa[i-1] + (h/2.0) * k1_XRa
 +
 +
    k2_XR = func_XR_prime(t1,XR1,CY1,XRa1,A[i-1])
 +
    k2_CY = func_CY_prime(t1,XR1,CY1,XRa1,A[i-1])
 +
    k2_XRa = func_XRa_prime(t1,XR1,CY1,XRa1,A[i-1])
 +
   
 +
   
 +
    #second step
 +
    t2 = t[i-1] + (h/2.0)
 +
    XR2 = XR[i-1] + (h/2.0) * k2_XR
 +
    CY2 = CY[i-1] + (h/2.0) * k2_CY
 +
    XRa2 = XRa[i-1] + (h/2.0) * k2_XRa
 +
   
 +
    k3_XR = func_XR_prime(t2,XR2,CY2,XRa2,A[i-1])
 +
    k3_CY = func_CY_prime(t2,XR2,CY2,XRa2,A[i-1])
 +
    k3_XRa = func_XRa_prime(t2,XR2,CY2,XRa2,A[i-1])
 +
   
 +
   
 +
    #third step
 +
    t3 = t[i-1] + h
 +
    XR3 = XR[i-1] + (h/2.0) * k3_XR
 +
    CY3 = CY[i-1] + (h/2.0) * k3_CY
 +
    XRa3 = XRa[i-1] + (h/2.0) * k3_XRa
 +
   
 +
    k4_XR = func_XR_prime(t3,XR3,CY3,XRa3,A[i-1])
 +
    k4_CY = func_CY_prime(t3,XR3,CY3,XRa3,A[i-1])
 +
    k4_XRa = func_XRa_prime(t3,XR3,CY3,XRa3,A[i-1])
 +
   
 +
   
 +
    #fourth step
 +
    average_k_XR = (1.0/6.0)*(k1_XR + 2.0*k2_XR + 2.0*k3_XR + k4_XR)
 +
    average_k_CY = (1.0/6.0)*(k1_CY + 2.0*k2_CY + 2.0*k3_CY + k4_CY)
 +
    average_k_XRa = (1.0/6.0)*(k1_XRa + 2.0*k2_XRa + 2.0*k3_XRa + k4_XRa)
 +
 +
    t[i] = t[i-1] + h
 +
    XR[i] = XR[i-1] + h * average_k_XR
 +
    CY[i] = CY[i-1] + h * average_k_CY
 +
    XRa[i] = XRa[i-1] + h * average_k_XRa
 +
   
 +
  #Plot
 +
 +
plot(t,XR,label='XR')
 +
plot(t,CY,label='CY')
 +
plot(t,XRa,label='XRa')
 +
plot(t,A,label='A')
 +
plt.xlabel('t(min)',size=20)
 +
plt.ylabel('proteins',size=20)
 +
legend()
 +
figure(figsize(15,10))
 +
plt.savefig("Shewanelladet.png", format='png',bbox_inches='tight',transparent=False)
 +
 +
</textarea>
 +
 +
<br><br>
 +
<h3> Stochastic Model </h3>
 +
<br><br>
 +
<p>Synechococcus elongatus</p>
 +
<textarea readonly rows = "20">
 +
 +
%pylab inline
 +
#This function 'decides' what happens in the Gillespie algorythm depending on the output of the second random number.
 +
def decider(random):
 +
        if(0<=random<cltve[1]):
 +
            LI.append(LI[i] + 60)
 +
            XI.append(XI[i] + 60)
 +
            EAi.append(EAi[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
        elif(cltve[1]<=random<cltve[2] and LI[i] != 0 ):
 +
            LI.append(LI[i] - 1)
 +
            XI.append(XI[i])
 +
            EAi.append(EAi[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
        elif(cltve[2]<=random<cltve[3] and XI[i] != 0):
 +
            LI.append(LI[i])
 +
            XI.append(XI[i]-1)
 +
            EAi.append(EAi[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
        elif(cltve[3]<=random<cltve[5]):
 +
            EAi.append(EAi[i] + 60)
 +
            LI.append(LI[i])
 +
            XI.append(XI[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
        elif(cltve[5]<=random<cltve[6] and EAi[i]!=0):
 +
            EAi.append(EAi[i] - 1)
 +
            LI.append(LI[i])
 +
            XI.append(XI[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
        else:
 +
            LI.append(LI[i])
 +
            XI.append(XI[i])
 +
            EAi.append(EAi[i])
 +
            CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3)
 +
 +
#The array t1 will contain all of the time intervals calculated with the tau formula
 +
    t1 = [0.0]
 +
 +
    #An array for each of the protein concentrations is initialized
 +
    LI = [0.0]
 +
    XI=[0.0]
 +
    CL=[0.0]
 +
    EAi=[0.0]
 +
   
 +
    # All of the constants involved in the differetial equations are established here
 +
    aCL = 0.0
 +
    bCL = 5.0
 +
    nCL = 2.0
 +
    kCL = 3000.0
 +
    gXI = 0.033
 +
    gLI = 0.033
 +
    aL = 1.0
 +
    bL = 5.0
 +
    kL = 3000.0
 +
    nL = 2.0
 +
    gEAi =  0.033
 +
 +
# This for loop iterates for 800'000 events. Each run-through, a time interval is calculated and added
 +
    #to the time array and each protein array is updated.
 +
    for i in range(800000):
 +
 +
        ks=[]
 +
        cltve=[]
 +
 +
        #LI events
 +
        k0 = aCL
 +
        k1 = ((bCL*pow(CL[i],nCL))/(pow(CL[i],nCL)+pow(kCL,nCL)))
 +
        k2 = gLI*LI[i]
 +
        ks.append(k0)
 +
        ks.append(k1)
 +
        ks.append(k2)
 +
 +
        #XI Events
 +
        k3 = gXI*XI[i]
 +
        ks.append(k3)
 +
 +
 +
        #EAi Events
 +
        k4 = aL
 +
        k5 = (bL/(1+pow((LI[i]/kL),nL)))
 +
        k6 = gEAi*EAi[i]
 +
        ks.append(k4)
 +
        ks.append(k5)
 +
        ks.append(k6)
 +
       
 +
        #s will represent the sum of all events
 +
       
 +
        s=0
 +
 +
        for j in ks:
 +
                s = s+j
 +
       
 +
        for j in range(len(ks)):
 +
            if(j==0):
 +
                cltve.append(ks[0]/s)
 +
            else:
 +
                cltve.append(cltve[j-1] + ks[j]/s)
 +
 +
        r1 = random.random()
 +
       
 +
        #We calculate the time interval for the next event to happen
 +
       
 +
        T = (1/s)*log(1/r1) + t1[i]
 +
       
 +
        #The time interval is added to the time array
 +
       
 +
        t1.append(T)
 +
       
 +
        #This random number will decide which event is chosen.
 +
       
 +
        r2 = random.random()
 +
       
 +
        #This random number is used to generate some noise in the input signal.
 +
       
 +
        r3 = (random.random()*1000)-500
 +
       
 +
        #This recalls the function to decide which event happens.
 +
       
 +
        decider(r2)
 +
 +
figure(figsize(15,10))
 +
plot(t1,CL,label='CL')
 +
plot(t1,XI,label='XI')
 +
plot(t1,LI,label='LI')
 +
plot(t1,EAi,label='EAi')
 +
plt.xlabel('Time (mins)', fontsize = 20)
 +
plt.ylabel('# of molecules' , fontsize = 20)
 +
plt.title('Stochastic simulation', fontsize = 30)
 +
legend(fontsize = 15)
 +
savefig('cyano.png')
 +
show()
 +
 +
</textarea>
 +
 +
<br><br>
 +
<p>Shewanella oneidensis</p>
 +
<textarea readonly rows = "20">
 +
%pylab inline
 +
 +
#We initialize the time array t2, the arrays for proteins and establish
 +
#the constants that will be used in the equations.
 +
 +
t2  = [0.0]
 +
 +
XR = [0.0]
 +
XR2 = [0.0]
 +
CY =[0.0]
 +
A = [0.0]
 +
 +
aXR = 10
 +
bXR = 5.0 
 +
kXR = 3000.0
 +
gXR = 0.033
 +
dXR2 = 0.1998
 +
gXR2 = 0.033
 +
aX = 10
 +
bX = 100
 +
nX = 2.0
 +
kX = 10000
 +
gCY = 0.25
 +
kr1 = 0.00015
 +
 +
 +
# This for loop iterates for 800'000 events. Each run-through, a time interval is calculated and added
 +
#to the time array and each protein array is updated.
 +
for i in range(12800000):
 +
   
 +
    ks=[]
 +
    cltive=[]
 +
   
 +
    #XR events
 +
   
 +
    k0 = aXR
 +
    k1 = kr1*XR[i]*A[i]
 +
    k2 = gXR*XR[i]
 +
    k3 = dXR2*XR2[i]
 +
    ks.append(k0)
 +
    ks.append(k1)
 +
    ks.append(k2)
 +
    ks.append(k3)
 +
   
 +
    #XR2 events
 +
             
 +
 
 +
    k4 = gXR2*XR2[i]
 +
    ks.append(k4)
 +
 
 +
   
 +
    #CY events
 +
   
 +
    k5 = aX
 +
    k6 = (bX*pow(XR2[i],nX))/(pow(kX, nX) + pow(XR2[i],nX))
 +
    k7 = gCY*CY[i]
 +
    ks.append(k5)
 +
    ks.append(k6)
 +
    ks.append(k7)
 +
 +
    #s will represent the sum of all events
 +
       
 +
    s = 0
 +
             
 +
    for j in ks:
 +
        s = s+j
 +
             
 +
    for j in range(len(ks)):
 +
        if(j==0):
 +
            cltive.append(ks[0]/s)
 +
        else:
 +
            cltive.append(cltive[j-1] + ks[j]/s)
 +
   
 +
    r1 = random.random()
 +
   
 +
    #We calculate the time interval for the next event to happen
 +
   
 +
    T = (1/s)*log(1/r1) + t2[i]
 +
   
 +
    #The time interval is added to the time array
 +
   
 +
    t2.append(T)
 +
   
 +
    #This random number will decide which event is chosen.
 +
   
 +
    r2 = random.random()
 +
 +
    #This function 'decides' what happens in the Gillespie algorythm depending
 +
    #on the output of the second random number.
 +
   
 +
    def decider(random):
 +
        if(0<=random<cltive[0]):
 +
            XR.append(XR[i] + 60)
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[0]<=random<cltive[1] and XR[i] != 0):
 +
            XR.append(XR[i] -1 )   
 +
            XR2.append(XR2[i] + 1)
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[1]<=random<cltive[2] and XR[i] != 0):
 +
            XR.append(XR[i] - 1)   
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[2]<=random<cltive[3] and XR2[i] !=0):
 +
            XR.append(XR[i] +1) 
 +
            XR2.append(XR2[i] -1)
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[3]<=random<cltive[4] and XR2[i] !=0):
 +
            XR.append(XR[i])   
 +
            XR2.append(XR2[i] -1)
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[4]<=random<cltive[5]):
 +
            XR.append(XR[i])   
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i] + 60)
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[5]<=random<cltive[6]):
 +
            XR.append(XR[i])   
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i] +60)
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        elif(cltive[6]<=random<cltive[7] and CY[i] != 0):
 +
            XR.append(XR[i])   
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i] - 1)
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
        else:
 +
            XR.append(XR[i])   
 +
            XR2.append(XR2[i])
 +
            CY.append(CY[i])
 +
            A.append(4000*sin(2*3.141592*T/1440)+4000)
 +
       
 +
   
 +
    #This recalls the function to decide which event happens.
 +
    decider(r2)
 +
 +
 +
figure(figsize(15,10))
 +
plot(t2,XR,label='XR')
 +
plot(t2,XR2,label='XR*')
 +
plot(t2,CY,label='CY')
 +
plot(t2,A,label='AHL')
 +
plt.xlabel('Time(mins)' , fontsize = 20)
 +
plt.ylabel('# of molecules', fontsize = 20)
 +
plt.title('Stochastic Simulation', fontsize = 30)
 +
legend(fontsize = 10)
 +
savefig('shewanellaestocasbX40.png')
 +
show()
 +
 +
</textarea>
 +
 +
</div>
  
 
<h4> Uploading pictures and files </h4>
 
<h4> Uploading pictures and files </h4>

Latest revision as of 03:54, 19 September 2015

iGEM Uniandes-Colombia

Team Project Wet Lab Dry Lab Hardware Human Practices Collaborations -

Mathematical Models



We use a mathematical model to check if the design works before starting to work at the laboratory, or improve the response of the original construct. To develop this model, the first step was to create a deterministic model, which was based on differential equations. This type of model describes the mean behavior for each of the substances in the synthetic circuit over time. However, it does not take into account the probabilities involved in each of the events described, the population interactions or the noise of the system.

The deterministic model is based on the law of mass conservation and expresses the inputs and outputs of the system with expressions that use the law of mass action and known models like Hill's or Michaelis Menten.However, we only have a model that shows a response that does not take into account the stochasticity of Nature. That's why did a second simulation: The stochastic Model. You are very welcome to check it all.





Differential equations



Synechococcus elongatus



Our clock protein binds to our promoter(pCL) and then transcribes LuxI and LacI proteins. We have to take into account the degradation(g) and the diffusion coefficient(c) if it is needed. After that, the two proteins go through independent paths.



Lux I Equation

LuxI has a basal production (alpha), a degradation rate (gamma), and is positively regulated by the clock protein. This positive regulation is represented as a hill equation for activated genes, represented through the second term.

$$ \frac{dXI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{XI}*XI$$

The product of luxI catalyzes the production of AHL



Lac I Equation

The terms that describe la I are analogous to those of luxI. There is a basal production rate (alpha), a degradation rate (gamma), and a term describing lacI production due to positive regulation by the clock protein (hill equation for genes that are positively regulated).

$$ \frac{dLI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{LI}*LI$$

Intracellular AHL-degrading enzyme equation

This enzyme, encoded by the aaiA gene, has a basal production (alpha), a degradation rate (gamma), a term accounting for how the negative feedback due to lacI (hill equation for genes with a negative regulator) influences the enzyme production, and a negative term (c) due to difussion outside the cell.



$$ \frac{dEA_{i}}{dt}=a_{L}+\frac{b_{s}}{1+(\frac{LI}{k_{L}})^{n_{L}}}-g_{LI}*LI$$

Shewanella



LuxR

LuxR has a basal production (alpha), a degradation rate (gamma), a negative term due to its coupling to AHL, and a positive term due to its decoupling from AHL.



$$\frac{dXR}{dt}=a-b_{XR}*XR*A-g_{XR}*XR+d_{XRa}*XRa$$

LuxR-AHL complex

The formation of the complex depends on a formation rate (ba) and the concentrations of LuxR (XR) and AHL (A). It also has a degradation rate (gamma), and a negative term due to decoupling of the complex (at a rate dXR).



$$\frac{dXRa}{dt}=b_{XR}*XR*A-g_{XRa}*XRa+d_{XR}*XRa$$

Cytochrome Equation

Cytochromes have a basal production (alpha), a degradation rate (gamma), and a production due to the attachment of the LuxR-AHL complex to the promoter.



$$\frac{dCY}{dt}=a_{X}+k_{c}*XR*A-g_{CY}*XR$$

Parameters



The parameters used in our simulation can be found in the table below:



Tablaparcol.png

Deterministic model



Pclock varies sinusoidally with time. That's why a sinusoidal input was given for it.



Synechococcus elongatus



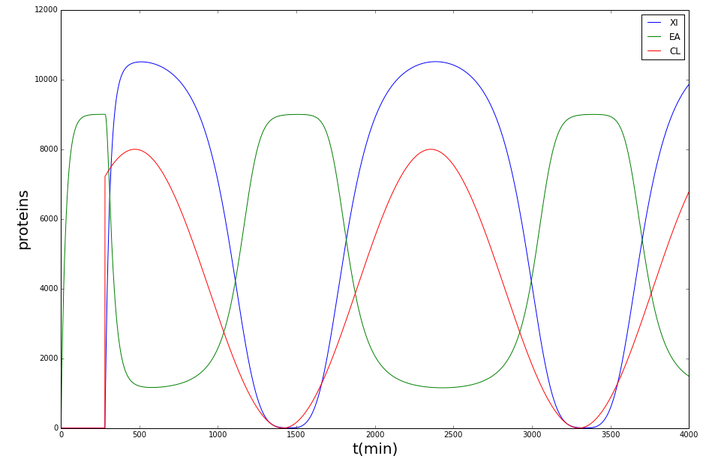
Cyanodet.png

As evidenced in the graph above, AHL also behaves sinusoidally as an output. Consequently, it is logical to have a sine wave with a 24hr period as input for Shewanella oneidensis



Shewanella oneidensis



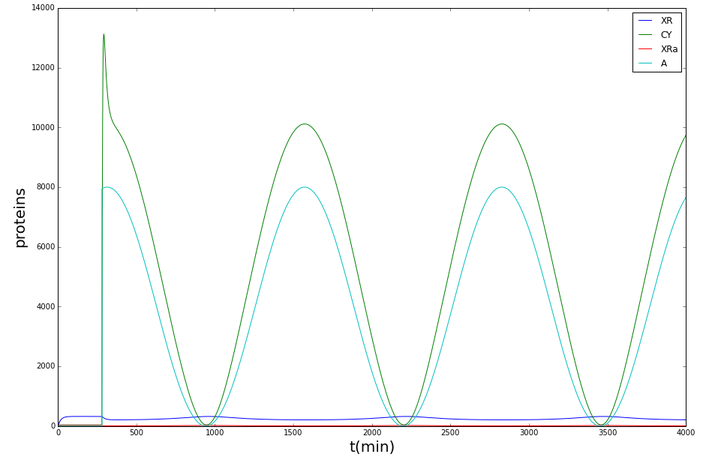
Shdef.png

It was thus shown that with the given parameters, the cytochromes (and so the resistance) in Shewanella






Stochastic model

Until now, all we have is a deterministic model of our system. This model takes into account exact concentrations of molecules as the variables in the differential equations. This means that all the calculations were made taking into account the mean values of the concentrations of particles.

Although this is a good approach, modelling the biological processes as random, stochastic events reflects a more accurate version of reality.

The following passage by physicist Daniel Gillespie provides some insight on this claim:

“…For “ordinary” chemical systems in which fluctuations and correlations play no significant role, the method stands as an alternative to the traditional procedure of numerically solving the deterministic reaction rate equations. For nonlinear systems near chemical instabilities, where fluctuations and correlations may invalidate the deterministic equations, the method constitutes an efficient way of numerically examining the predictions of the stochastic master equation. Although fully equivalent to the spatially homogeneous master equation, the numerical…” (Gillespie 1976)

To tackle this problem, Daniel Gillespie designed the stochastic simulation algorithm. This method is particularly useful when reducing computational costs.

The algorithm is based on the reaction probability density function; a function that essentially dictates the amount of time that will pass between events such as the creation or degradation of a protein. This time interval is given by the equation:

$$\tau =\frac{1}{\sum n_{events}}*ln\left ( \frac{1}{random number} \right )$$

The algorithm is based on the reaction probability density function; a function that essentially dictates the amount of time that will pass between events such as the creation or degradation of a protein.

To determine which event will occur, a second random number from 0 to 1 is used. After the events are normalized, depending where in the range of the event normalization the random number falls, a particular event is chosen.

The following graphs display the outcome of the simulations for Synechococcus elongatus and Shewanella oneidensis.



Synechococcus elongatus

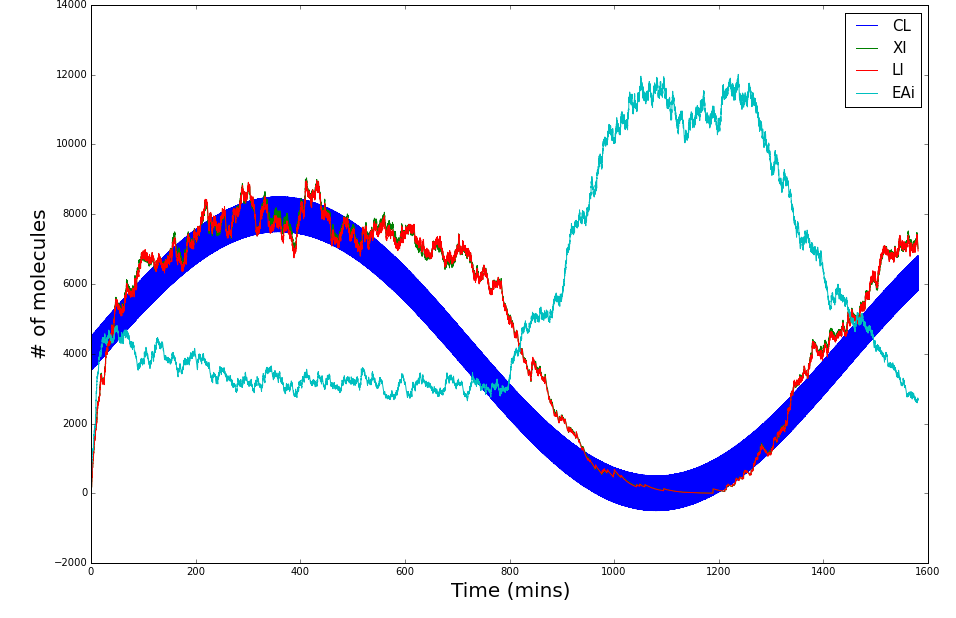
Cyano.png
Figure 1


Shewanella oneidensis

ShewanellaestocasbX40.png
Figure 2


Scripting



Deterministic Model



Synechococcus elongatus



Shewanella onediensis



Stochastic Model



Synechococcus elongatus



Shewanella oneidensis

Uploading pictures and files

You can upload your pictures and files to the iGEM 2015 server. Remember to keep all your pictures and files within your team's namespace or at least include your team's name in the file name.
When you upload, set the "Destination Filename" to Team:YourOfficialTeamName/NameOfFile.jpg. (If you don't do this, someone else might upload a different file with the same "Destination Filename", and your file would be erased!)

CLICK HERE TO UPLOAD FILES