Team:UT-Tokyo/Project

• PROJECT
  INTRO STRATEGY SYSTEM RESULT APPLICATION
• MODEL
  TOP SYSTEM SYSTEM2 MATHEMATICS PARAMS
• EXPERI.
  LABNOTE PROTOCOL

• HOME

• ACHIEV.
• PRACT.
  OVERVIEW PROBLEM SOLVING PUBLIC PARTICIPATION
• TEAM

INTRODUCTION

Project Overview

Mechanisms for development of living things have been investigated for a long time. In 1952, Alan Turing made a key contribution. He showed that the interaction of two substances with different diffusion rates can generate spatial patterns of the concentration, which are called Turing Patterns, without any preformed pattern[1]. This pattern can be a base for development. The idea has been applied to explain periodical patterns such as hair follicle distribution of mice[2], stripe formation on zebrafish[3].

Fig.I

Here, we tried to reconstruct Turing Pattern by Escherichia coli in a way of synthetic biology to understand the mechanism more. E. coli has cell-cell communication system called quorum sensing. Utilizing this system, we aimed to generate a periodical colony pattern. This project leads to further understanding of Turing Pattern, especially characteristics of Turing Pattern generated by genetic circuits. It points the way to understanding of development of living things, thus can be applied to tissue formation.

Fig.II

Approach

Below is the flow of our project.

1. 1. Develop a strategy for pattern formation using mathematical modeling.

2. 2. Experimentally measure parameters to modify the model.

3. 3. Fix experimental conditions according to modeling results.

4. 4. Generate colony patterns and verify the model by comparing patterns.

Fig.III

Turing Mechanism

Turing Pattern is generated by the interaction of two substances with different diffusion rates. These substances are called activator and inhibitor. Activator promotes its own production and the production of inhibitor, and inhibitor inhibits the production of activator(Fig.1). Inhibitor diffuses faster than activator.

Fig.1 Turing mechanism The interaction of activator and inhibitor generates patterns.

Turing focused on the difference in the diffusion rates, but later Meinhardt and Gierer explained the mechanism from the point of local self-activation and lateral inhibition[4]. This explanation is easy to understand intuitively, so we will explain Turing pattern along this explanation.

Fig.2 The generation of a periodical pattern
The initial condition is (a), and as time passes, a periodical concentration pattern is generated((b)~(f)).

At first, there is no preformed pattern in the field and the concentrations of two substances are homogeneous through the field (Fig. 2 (a)). However, there can be a spot with a little bit high concentration of activator because of perturbation. At such a point, the concentration of activator becomes higher and higher, as well as that of inhibitor, by the function of activator (Fig. 2 (b)~(c)). This corresponds to local self-activation. Since inhibitor diffuses faster than activator, the concentration of inhibitor becomes relatively high around that point and that of activator becomes low because of the inhibitory effect of inhibitor there (Fig. 2 (d)~(e)). This corresponds to lateral inhibition. Therefore, a spot of activator is generated. This reaction occurs at different points in the field, and the distance between each spot is regulated by the interaction of the two substances (Fig. 2 (f)). In this way, a periodical pattern is generated in the field.

Advantage Of Synthetic Biological Approach

Pattens of living things have been investigated for a long time, but it was not easy to prove directly if these patterns are produced by the reaction-diffusion systems or another mechanism because living systems are so complex. Biologists still face a big problem: how activator and inhibitor interacts in vivo. We have little information about what interactions between them generate what patterns. If we can control the interactions, the relation between interactions and patterns can be revealed. We therefore reconstructed a Turing system using two advantages of synthetic biology; controllability and biological directness. We can change the diffusion rate of E. coli and the strength of inhibitory effects of inhibitor by inducing synthetic circuit, which can be a great advantage of the experimental system. Chemical system has a similar advantage, but it is far from living systems. For example, it does not include processes of transcription and translation, which is necessary for living things, through the interaction of two factors. Our system uses cells themselves for pattern formation, so it may be directly applied to developmental studies and point the way to tissue formation.

STRATEGY

As explained in the part of Introduction, the system of Turing pattern is based on the interaction between two factors; activator and inhibitor. To achieve the formation of Turing pattern, two conditions are required on this system.

1. When the diffusion effect is negligible, the system is monostable; the concentrations of two factors take a constant value throughout the field (Fig. 1 (a)).
2. When diffusion introduced, the system became bistable; the concentrations of two factors take either of two values according to the position on the field (Fig. 1 (b)).

Fig. 1 Two conditions for generating Turing Pattern
(a) Condition 1: When the diffusion effect is negligible, the system is monostable.
(b) Condition 2: When the diffusion effect is considerable, the system is bistable.

These conditions were derived from the mathematical modeling of the mechanism, and the detail is shown in the part of Modeling.

We established a strategy which satisfies the two conditions for pattern formation using mathematical modeling.

Basic Strategy

The first one is based on Turing’s classic model.(Figure1)

Fig.1 Model 1
Imitation of Turing's classic model performed by Escherichia coli and AHL.

Here, we consider the “reaction” between E. Coli and AHL. AHL is a type of intercellular signaling molecule that can promote transcription from specific promoter when its concentration in a cell gets higher than a certain threshold. This system is called ”Quorum Sensing”. And here, AHL is set to induce protein which inhibits the multiplication of E. Coli.

E. coli produces AHL, and AHL inhibits the increase of E. coli. E. coli also reproduces.

Diffusion rate of AHL is large because its size and molecular weight are quite small. On the other hand, the rate of E. coli should be low in order to form Turing pattern. To achieve this, we modified E. coli by knocking out certain gene concerned with its motility.

This model can be divided into two sections, and here, let's call them control loop 1, and control loop 2.

Figure 1-1 shows the control loop 1. This loop is negative feedback, and when the concentration of E.coli increases in a certain position, the concentration of AHL also increases around there. Then AHL diffuses fast, inhibits the multiplication of E.coli in some long distance from the position. This kind of control loop is called long-range negative feedback loop.

Fig.1-1 Control loop 1
This loop is long-range negative feedback, and it drives lateral inhibition when the concentration of E. Coli gets higher.

Figure 1-2 shows the control loop 2. E. coli repruduces, so this loop can be considered as positive feedback. In addition, E. coli reproduces near of its position, for the diffusion rate of E. coli is small. This kind of control loop is called short-range positive feedback loop.

Fig.1-2 Control loop 2
This loop is short-range positive feedback, and it drives local activation when the concentration of E. Coli gets higher.

We conducted mathematical modeling of this system to see whether this system generates patterns we expected. However, it revealed that this system may not satisfy the condition 2 explained on the top of this part.

1. When the diffusion effect is negligible, the system is monostable; the concentrations of two factors take a constant value through the field.
2. When the diffusion effect is considerable, the system became bistable; the concentrations of two factors take either of two values according to the position on the field.

Note that mathematical modeling is just a model and does not completely reflect the reality, so this result does not rule out the possibility that this system forms patterns.

Analyzing the condition 2 mathematically, it turns out that this system has one potential defect: the order of the growth rate of E. coli is expected to be expressed to depend linearly on the concentration of E. coli, resulting in primary order multiplication whereas greater changes of the increase rate is required in Turing’s model. In other words, there has to be concentration difference of E. coli depending on the position on the field.

To solve this problem, we introduced a mutual inhibition by adding another type of E. coli as co-activator.

Improved Strategy

Fig.2 Model 2:
Improved model from Model 1

E. Coli(activator) activates AHL, and AHL inhibits E. Coli, as in the model in Figure 1. This loop functions as lateral inhibition.(Figure2-1)

Fig.2-1 Long-range negative feedback loop
Same loop as in Figure 1-1

In order to make a spacial difference of the concentration of activator, another type of E. coli (co-activator) is added to Basic Strategy.
Two types of E. Coli (activator and co-activator) inhibit each other(Figure2-2), and this interaction is achieved by the function of the protein called Colicin and growth competition. (The detail is shown in the chapter of System.)

Fig.2-2 Short-range positive feedback loop
Mutual inhibition forms positive feedback. And the slow diffusion rate of the agent substance(Colicin) makes the range of this loop short.

Co-activator produces Colicin, which represses the growth of activator. The growth rate of co-activator is modulated to be lower than that of activator. Therefore, if co-activator does not produce Colicin, activator can survive and grow, but co-activator cannot because it loses growth competition. The growth competition is caused by the scramble for nutrients and space to grow. This means that activator can be assumed to have an inhibitory effect on co-activator. As a result, a mutual inhibition is formed between activator and co-activator.

In this interaction, the increase of activator causes the decrease of co-activator, and the decrease of co-activator causes the increase of activator in turn. The diffusion rate of Colicin is small, for its size and molecular weight are large [5]. Therefore, we can regard it as short-range positive feedback loop.

The growth rate induced by this positive feedback is much higher than that of self-multiplication of the model in the Basic Strategy, so concentration difference of E. coli can be made.

Also, Mathematical modeling shows that this system can satisfy the two conditions.

1. When the diffusion effect is negligible, the system is monostable; the concentrations of two factors take a constant value through the field.
2. When the diffusion effect is considerable, the system became bistable; the concentrations of two factors take either of two values according to the position on the field.

SYSTEM

In this chapter, we give concrete constructions for the concepts explained at Strategy. First, we explain basic mechanisms which are necessary to understand our construction.

1. Motility control

1.1 CheZ

By regulating the diffusion rate, we can control what pattern is generated.The motility of E. coli is regulated by CheZ. When CheZ is expressed, E. coli swims straight and the diffusion rate is high. When CheZ is not expressed, E. coli tumbles and the diffusion rate is low (Fig. 1.1).
In our project, we used cheZ knock out strain (JW1870), and controlled the diffusion rate of E. coli by transffering cheZ.

Fig.1-1 Swimming phase and tumbling phase
The motility of the cell is regulated by CheZ.
(a)Swimming phase: CheZ is expressed and inhibits CheY.
(b)Tumbling phase: CheY binds to flagellar binding proteins.

The movement of E. Coli is roughly divided in two phases, swimming(a) and tumbling(b). In order to convert these phases, E. Coli use flagellar binding protein called CheY which is controlled by CheZ. Under the expression of CheZ, CheY is dephosphorylated by CheZ and inactivated to bind to the flagellar mortar proteins. Consequently, the rotation of flagellar is changed and cell initiates swimming phase.[7]
In our project, we use cheZ knock out strain (JW18XX), and transfer cheZ under inducible promoter to control cell motility.

Detail Explanation

The movement of E. coli is roughly divided in two phases, swimming(a) and tumbling(b). In order to convert these phases, E. coli use flagellar binding protein called CheY which is controlled by CheZ. Under the expression of CheZ, CheY is dephosphorylated by CheZ and inactivated to bind to the flagellar motor proteins. Consequently, the rotation of flagellar is changed and cell initiates swimming phase.[1]

2. Cell-Cell interaction

We can also control what pattern is generated by regulating the growth rate of E. coli. We planned to regulate the rate using cell-cell interactions.

2.1 AHL

Fig.2-1 Quorum sensing
Blue hexagon shows AHL molecule. When population density gets higher than certain treshold, the transcription from specific promoter(such as Plux) is enhanced.

One of the cell-cell interactions is played by AHL.
AHLs are signal molecules involved in bacterial quorum sensing (Fig 2.1). AHL can easily permeate cell membranes and can regulate the transcription of target cell. For example, in Lux system, AHL binds to LuxR dimer and that complex enhances transcription from PRlux promoter.

2.2 Colicin

Fig.2-2 Mechanism of Colicin release
※This figure may a littel bit differ from actual mechanism.

Colicin E3 (ColE3) cleaves 16SrRNA at a specific site. Colicin E3 Immunity protein (ColI) binds to ColE3 and neutralizes it. Colicin Lysis protein (ColL) allows ColE3 to pass thorugh the cell membrane. The mechanism of colicin release has not been elucidated.[7][8]

The another cell-cell interaction is played by Colicin.
Colicin E3 is a cytotoxin which are released to environment and kill other related strains. It requires Colicin Lysis protein (ColL) to pass through the cell membrane. Colicin Immunity protein (ColI) neutralizes the cytotoxicity of Colicin E3.

Detail Explanation

Colicin is a cytotoxin which is released to the environment and kills other related strains. Release of colicin involves one protein; Colicin Lysis Protein (ColL). Colicin lysis protein allows colicins to be released. The mechanism how the colicin lysis protein allows colicin release has not been fully elucidated, but it is sure that this protein raise membrane permeability and cause quasilysis.[2] After Colicin released, they diffuse through the medium and bind to the receptor on the target cell membrane. Then, they are imported to the cytoplasm or cytoplasmic membrane of target cell by Tol-system or Ton-system. (If you want to know the mechanism of the Colicin import, see [2]) Colicin producing cells also express Colicin Immunity Protein (ColI) in order to protect themselves from the cytotoxicity of Colicin. Colicins have various cytotoxicity such as DNase activity, RNase activity or Pore forming across the inner membrane. In our project, we select colicin E3 because it has low risk of safety problems. Colicin E3 specifically digests 16S rRNA which is only in bacteria.

3. Detailed overall system

Basic Strategy

Fig.3-1 Construction for Basic Strategy
Positive feed back loop, which is necessary for local activation, is played by multiplication of E. coli.

Gene modified E. Coli is an activator, and AHL is an inhibitor.
Local activation is played by self-reproducing of E. Coli.
Lateral inhibition is played by AHL. AHL activates the expression of Barnase (RNase Ba) which causes E. Coli to die. Barnase is the RNase from Bacillus amyloliquefaciens.
Since gene modified E. Coli is cheZ knock out strain, the difference between the diffusion rate of E. Coli and that of AHL is enough to generate Turing Pattern. However, as mentioned in Strategy section, this system may not generate Turing Pattern because the strength of the positive feedback of activator may not enough. Therefore, we improved this strategy by adding co-activator.

Improved Strategy

Fig 3.2 Construction for Improved Strategy

The inhibitory effect on co-activator from activator is caused by growth competition. When colicin sensitive cells, activator, grow faster than colicin producing cells, co-activator, and the initial concentration of activator is higher than a certain threshold, colicin sensitive cells continue to increase and colicin producing cells die[9].

RESULT

Motility Control

Diffusion rate of E.coli is one of the key factors for the control of pattern formation. As mentioned in System, diffusion rate can be changed by the strength of CheZ gene expression. We constructed several CheZ generators which express a different amount of CheZ gene and tried to measure the diffusion rate. The picture below shows the appearance of E.coli diffusing in semi solid agar which is prepared to be very soft (0.15%) for observing E.colidiffusion.

Fig.1 The photograph taken by time lapse photo. (left) 2 hours, (center) 11 hours, (right) 19 hours after starting photographing.

In previous iGEM project, some teams also utilized CheZ gene to control motility. However, they didn't measure the diffusion rate quantitatively. Here, we exploit time lapse photography and mathematical expression to quantitate the diffusion rate. According to mathematical analysis, E.coli colony expand in the speed determined by diffusion rate and growth rate. On the basis of this fact, we can determine diffusion rate by measuring colony expanding speed and growth rate.

Fig.2 Combination of measuring expanding speed and growth rate enables determination of the diffusion rate.

Expanding speed was determined by interval shooting of colony expansion and growth rate was determined by measuring OD600. The bar graph below shows the diffusion rate determined by our measurement strategy.
DNA constructs we used was CheZ strong 1 generator({{part:BBa_K1631018}}) , CheZ strong 2 generator({{part:BBa_K1631020}}), CheZ medium generator ({{part:BBa_K1631019}})and RFP generator({{part:BBa_J23101}})

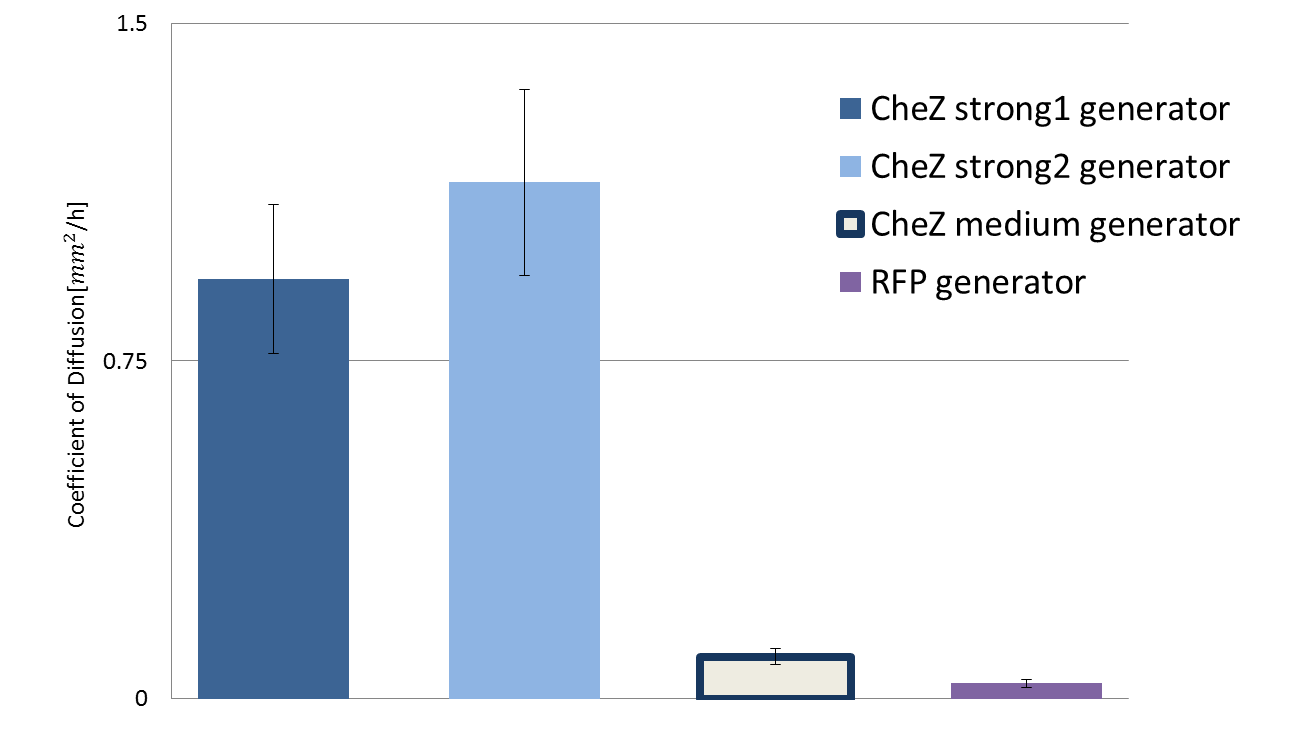
Fig.3 Diffusion rate according to different strength of CheZ expression

CheZ strong 1 generator and CheZ strong 2 generator showed high diffusion rate. In contrast, medium CheZ generator and RFP generator showed low diffusion rate. According to the parts registry featured constitutive promoter family, expression level of constitutive promoter of strong 1 is highest and that of medium is lowest among ] three promoter we used. This fact is consistent with the result we acquired.

In order to control the pattern, we confirmed that diffusion rate of E. coli can be regulated by CheZ. We also measured the diffusion rate of E. coli.

Growth Rate Control

In our system, lateral inhibition is played by Barnase and AHL.

First, we assay the function of Barnase.

We constructed({{part:BBa_K1631012}})and introduced it to JM109. IPTG+ means induction of 100μM IPTG..
We also measure the growth rate of Plac -rbs- GFP -d.term as negative control.
We measured OD600 of 3 samples for each condition

Fig.4 Growth repression by Barnase.

As, seen in figure 4, Barnase repress the growth of E. coli significantly. We also evaluated the growth rate of these samples by slope of next figure.

Plac GFP IPTG-	0.0219 [/min]
Plac GFP IPTG +	0.0205 [/min]
Plac Barnase GFP IPTG-	0.0222 [/min]
Plac Barnase GFP IPTG+	0.0117 [/min]

Bistability

In order to control the ColicinE3 release, we tried to regulate the expression of Colicin Lysis Protein. According to the previous reserach, [8].Colicin Lysis Protein cause quqsi-lysis and growth of E. coli is inhibited. We tried to confirm the quasi-lysis, but regardless of induction with 1mM IPTG, OD600 is decreased after about 4 hours. This maybe caused by the leak from lac promoter(BBa_R0011). It is considered that quasi-lysis is occuered at low expression level of Colicin Lysis Protein, and even if the expression level is bigger than that point, the effect to E. coli

Fig.5

APPLICATION

Tissue Regeneration

Our project gives data for two dimension dynamics of a specific network among cells. This data can help study of tissue formation, which is a pattern formation in three dimension. For a scaffold of pattern formation in three dimension, you can use 3D hydrogel instead of semi solid agar on a plate (Fig. 1)[10].

Fig. 1 Tissue regeneration by self-organization.
y interactions between cells in 3D hydrogel, a tissue may be formed. This figure is cited from the previous study[10].

REFERENCE

[1]Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London B: Biological Sciences, 237(641), 37-72.

[2]Sick, S., Reinker, S., Timmer, J., & Schlake, T. (2006). WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science, 314(5804), 1447-1450.

[3]Nakamasu, A., Takahashi, G., Kanbe, A., & Kondo, S. (2009). Interactions between zebrafish pigment cells responsible for the generation of Turing patterns. Proceedings of the National Academy of Sciences, 106(21), 8429-8434.

[4]Meinhardt, H., & Gierer, A. (2000). Pattern formation by local self-activation and lateral inhibition. Bioessays, 22(8), 753-760.

[5]Cascales, E. et al. (2007) Colicin Biology. Microbiology and Molecular Biology Reviews, 71(1), 158-229.

[6]Parkinson, J. S. (2003). Bacterial chemotaxis: a new player in response regulator dephosphorylation. Journal of bacteriology, 185(5), 1492-1494..

[7]Cascales, E., Buchanan, S. K., Duché, D., Kleanthous, C., Lloubes, R., Postle, K., ... & Cavard, D. (2007). Colicin biology. Microbiology and Molecular Biology Reviews, 71(1), 158-229.

[8]Lloubes, R., Bernadac, A., Houot, L., & Pommier, S. (2013). Non classical secretion systems. Research in microbiology, 164(6), 655-663.

[9]Chao, L., & Levin, B. R. (1981). Structured habitats and the evolution of anticompetitor toxins in bacteria. Proceedings of the National Academy of Sciences, 78(10), 6324-6328.

[10]Chen, T. H. (2014). Tissue Regeneration: From Synthetic Scaffolds to Self-Organizing Morphogenesis. Current stem cell research & therapy, 9(5), 432-443.

Sponsors

© iGEM UT-Tokyo. All rights reserved.