Team:Uniandes Colombia/DryLab

Mathematical Models

We use a mathematical model to check if the design works before starting to work at the laboratory, or improve the response of the original construct. To develop this model, the first step was to create a deterministic model, which was based on differential equations. This type of model describes the mean behavior for each of the substances in the synthetic circuit over time. However, it does not take into account the probabilities involved in each of the events described, the population interactions or the noise of the system.

The deterministic model is based on the law of mass conservation and expresses the inputs and outputs of the system with expressions that use the law of mass action and known models like Hill's or Michaelis Menten.However, we only have a model that shows a response that does not take into account the stochasticity of Nature. That's why did a second simulation: The stochastic Model. You are very welcome to check it all.

Differential equations

Synechococcus elongatus

Our clock protein binds to our promoter(pCL) and then transcribes LuxI and LacI proteins. We have to take into account the degradation(g) and the diffusion coefficient(c) if it is needed. After that, the two proteins go through independent paths.

Lux I Equation

LuxI has a basal production (alpha), a degradation rate (gamma), and is positively regulated by the clock protein. This positive regulation is represented as a hill equation for activated genes, represented through the second term.

$$ \frac{dXI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{XI}*XI$$

The product of luxI catalyzes the production of AHL

Lac I Equation

The terms that describe la I are analogous to those of luxI. There is a basal production rate (alpha), a degradation rate (gamma), and a term describing lacI production due to positive regulation by the clock protein (hill equation for genes that are positively regulated).

$$ \frac{dLI}{dt}=a_{s}+\frac{b_{s}*CL^{n_{s}}}{CL^{n_{s}+k_{s}^{n_{s}}}}-g_{LI}*LI$$

Intracellular AHL-degrading enzyme equation

This enzyme, encoded by the aaiA gene, has a basal production (alpha), a degradation rate (gamma), a term accounting for how the negative feedback due to lacI (hill equation for genes with a negative regulator) influences the enzyme production, and a negative term (c) due to difussion outside the cell.

$$ \frac{dEA_{i}}{dt}=a_{L}+\frac{b_{s}}{1+(\frac{LI}{k_{L}})^{n_{L}}}-g_{LI}*LI$$

Shewanella

LuxR

LuxR has a basal production (alpha), a degradation rate (gamma), a negative term due to its coupling to AHL, and a positive term due to its decoupling from AHL.

$$\frac{dXR}{dt}=a-b_{XR}*XR*A-g_{XR}*XR+d_{XRa}*XRa$$

LuxR-AHL complex

The formation of the complex depends on a formation rate (ba) and the concentrations of LuxR (XR) and AHL (A). It also has a degradation rate (gamma), and a negative term due to decoupling of the complex (at a rate dXR).

$$\frac{dXRa}{dt}=b_{XR}*XR*A-g_{XRa}*XRa+d_{XR}*XRa$$

Cytochrome Equation

Cytochromes have a basal production (alpha), a degradation rate (gamma), and a production due to the attachment of the LuxR-AHL complex to the promoter.

$$\frac{dCY}{dt}=a_{X}+k_{c}*XR*A-g_{CY}*XR$$

Parameters

The parameters used in our simulation can be found in the table below:

Deterministic model

Pclock varies sinusoidally with time. That's why a sinusoidal input was given for it.

Synechococcus elongatus

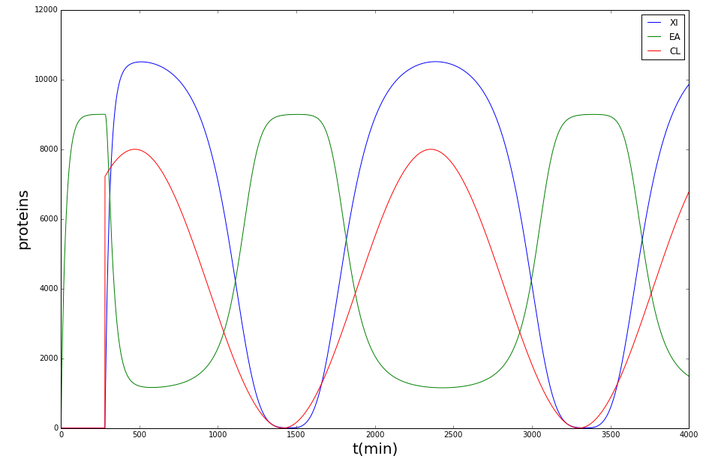
As evidenced in the graph above, AHL also behaves sinusoidally as an output. Consequently, it is logical to have a sine wave with a 24hr period as input for Shewanella oneidensis

Shewanella oneidensis

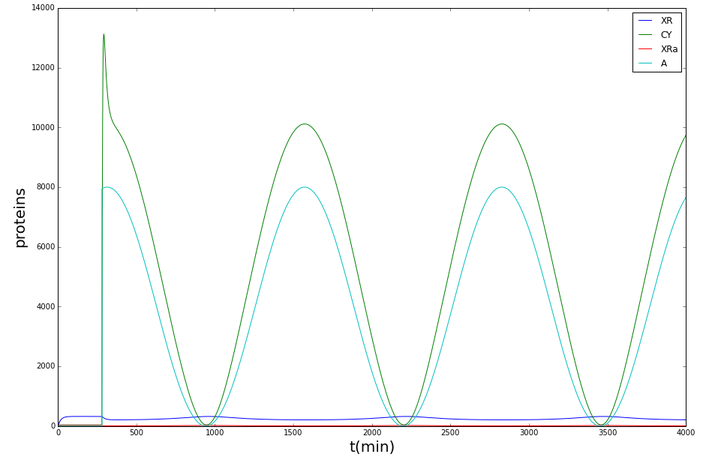
It was thus shown that with the given parameters, the cytochromes (and so the resistance) in Shewanella

Stochastic model

Until now, all we have is a deterministic model of our system. This model takes into account exact concentrations of molecules as the variables in the differential equations. This means that all the calculations were made taking into account the mean values of the concentrations of particles.

Although this is a good approach, modelling the biological processes as random, stochastic events reflects a more accurate version of reality.

The following passage by physicist Daniel Gillespie provides some insight on this claim:

“…For “ordinary” chemical systems in which fluctuations and correlations play no significant role, the method stands as an alternative to the traditional procedure of numerically solving the deterministic reaction rate equations. For nonlinear systems near chemical instabilities, where fluctuations and correlations may invalidate the deterministic equations, the method constitutes an efficient way of numerically examining the predictions of the stochastic master equation. Although fully equivalent to the spatially homogeneous master equation, the numerical…” (Gillespie 1976)

To tackle this problem, Daniel Gillespie designed the stochastic simulation algorithm. This method is particularly useful when reducing computational costs.

The algorithm is based on the reaction probability density function; a function that essentially dictates the amount of time that will pass between events such as the creation or degradation of a protein. This time interval is given by the equation:

$$\tau =\frac{1}{\sum n_{events}}*ln\left ( \frac{1}{random number} \right )$$

The algorithm is based on the reaction probability density function; a function that essentially dictates the amount of time that will pass between events such as the creation or degradation of a protein.

To determine which event will occur, a second random number from 0 to 1 is used. After the events are normalized, depending where in the range of the event normalization the random number falls, a particular event is chosen.

The following graphs display the outcome of the simulations for Synechococcus elongatus and Shewanella oneidensis.

Synechococcus elongatus

Figure 1

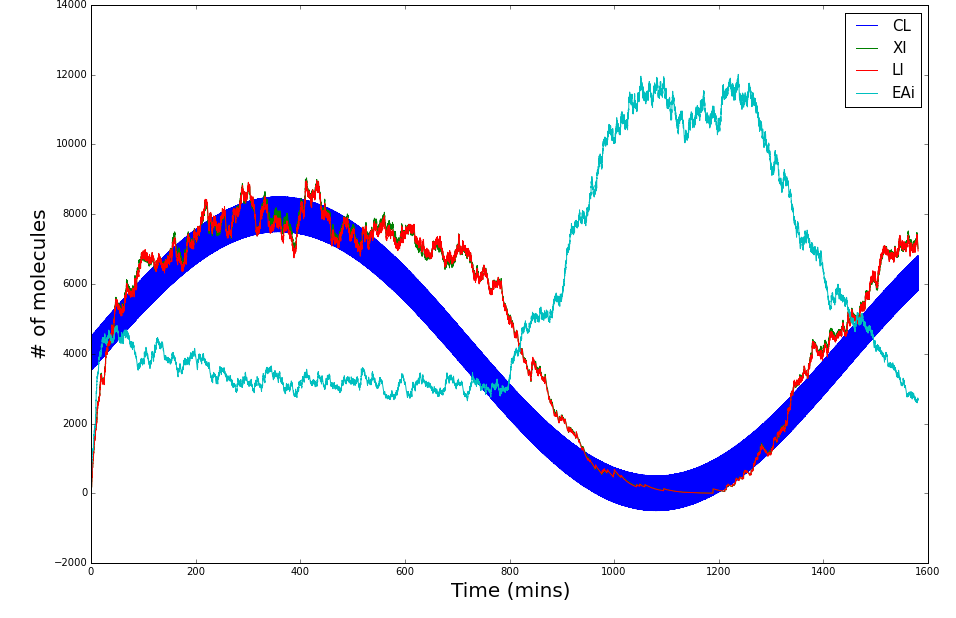
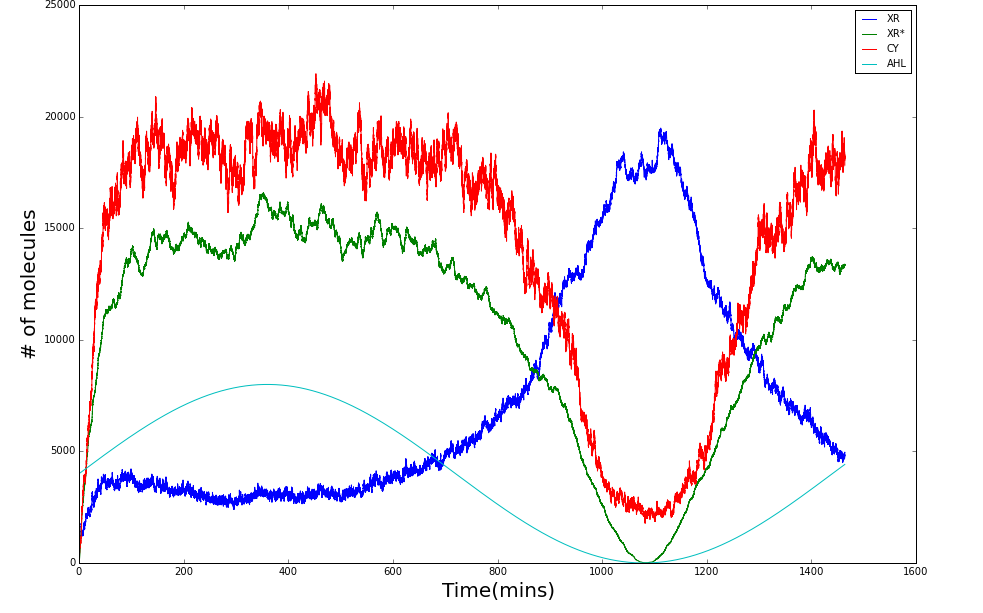
Shewanella oneidensis

Figure 2

Scripting

Deterministic Model

Synechococcus elongatus

%pylab inline #we define first the value of h and the corresponding range in x h=0.2 n_points = int((4000.0)/h) t = zeros(n_points) XI = zeros(n_points) LI = zeros(n_points) EA = zeros(n_points) CL = zeros(n_points) gLI=0.0231 size(CL) #definimos todas las ecuaciones def func_XI_prime(t,XI,LI,EA,CL): return 0+((400*pow(CL,2))/(pow(CL,2)+pow(3000,2)))-(1/30.0)*XI def func_LI_prime(t,XI,LI,EA,CL): return 5+((300*pow(CL,2))/(pow(CL,2)+pow(4000,2)))-(gLI)*LI def func_EA_prime(t,XI,LI,EA,CL): return 1+((300)/(1.0+(pow(LI,2)/pow(4000,2))))-(1/30.0)*EA t[0] = 0.0 XI[0] = 0.0 LI[0] = 0.0 EA[0] = 0.0 CL[0] = 0.0 for i in range(1400): CL[i]=0.0 for i in range(1401,n_points): CL[i]=4000*sin(t[i]/300)+4000 for i in range(1,n_points): k1_XI = func_XI_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1]) k1_LI = func_LI_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1]) k1_EA = func_EA_prime(t[i-1],XI[i-1],LI[i-1],EA[i-1],CL[i-1]) #first step t1 = t[i-1] + (h/2.0) XI1 = XI[i-1] + (h/2.0) * k1_XI LI1 = LI[i-1] + (h/2.0) * k1_LI EA1 = EA[i-1] + (h/2.0) * k1_EA k2_XI = func_XI_prime(t1,XI1,LI1,EA1,CL[i-1]) k2_LI = func_LI_prime(t1,XI1,LI1,EA1,CL[i-1]) k2_EA = func_EA_prime(t1,XI1,LI1,EA1,CL[i-1]) #second step t2 = t[i-1] + (h/2.0) XI2 = XI[i-1] + (h/2.0) * k2_XI LI2 = LI[i-1] + (h/2.0) * k2_LI EA2 = EA[i-1] + (h/2.0) * k2_EA k3_XI = func_XI_prime(t2,XI2,LI2,EA2,CL[i-1]) k3_LI = func_LI_prime(t2,XI2,LI2,EA2,CL[i-1]) k3_EA = func_EA_prime(t2,XI2,LI2,EA2,CL[i-1]) #third step t3 = t[i-1] + h XI3 = XI[i-1] + (h/2.0) * k3_XI LI3 = LI[i-1] + (h/2.0) * k3_LI EA3 = EA[i-1] + (h/2.0) * k3_EA k4_XI = func_XI_prime(t3,XI3,LI3,EA3,CL[i-1]) k4_LI = func_LI_prime(t3,XI3,LI3,EA3,CL[i-1]) k4_EA = func_EA_prime(t3,XI3,LI3,EA3,CL[i-1]) #fourth step average_k_XI = (1.0/6.0)*(k1_XI + 2.0*k2_XI + 2.0*k3_XI + k4_XI) average_k_LI = (1.0/6.0)*(k1_LI + 2.0*k2_LI + 2.0*k3_LI + k4_LI) average_k_EA = (1.0/6.0)*(k1_EA + 2.0*k2_EA + 2.0*k3_EA + k4_EA) t[i] = t[i-1] + h XI[i] = XI[i-1] + h * average_k_XI LI[i] = LI[i-1] + h * average_k_LI EA[i] = EA[i-1] + h * average_k_EA if (i < 1400): CL[i]=0.0 if (1401<i<n_points): CL[i]=4000*sin(t[i]/300)+4000 plot(t,XI,label='XI') #plot(t,LI,label='LI') plot(t,EA,label='EA') plot(t,CL,label='CL') plt.xlabel('t(min)',size=20) plt.ylabel('proteins',size=20) legend() figure(figsize(15,10)) plt.savefig("Cyanodet.png", format='png')

Shewanella onediensis

%pylab inline #First,we define the value of h,the corresponding range in x and the constants #If you need more information about the parameters of our model please visit our Wiki. h=0.2 #step value a=10.0 bXR=5.0 kXR=3000.0 gXR=0.06 dXRa=0.1980 #actived XR aX=10.0 bX=100.0 kc=0.0015 nX=2.0 kx=10000.0 gCY=0.25 kXRa=3000.0 gXRa=0.0231 dXR=10.0 n_points = int((4000.0)/h) #Here we create the the arrays that represent the variables in the differential equations. t = zeros(n_points) XR = zeros(n_points) CY = zeros(n_points) XRa = zeros(n_points) A = zeros(n_points) #we define all the functions def func_XR_prime(t,XR,CY,XRa,A): return a +((bXR)/(1.0+(A/kXR)))-(gXR*XR)+(dXRa*XRa) def func_CY_prime(t,XR,CY,XRa,A): return aX+(kc*A*XR)-(gCY*CY) def func_XRa_prime(t,XR,CY,XRa,A): return (bXR/(1.0+(A/kXR)))-(gXRa*XRa)-(dXRa*XRa) #First we initialize the arrays t[0] = 0.0 XR[0] = 0.0 CY[0] = 0.0 XRa[0] = 0.0 A[0] = 0.0 #then we determine the input function for i in range(1400): A[i]=0.0 for i in range(1401,n_points): A[i]=4000*sin(t[i]/200)+4000 #And finally we do 4th order Runge Kutta. for i in range(1,n_points): if (i < 1400): A[i]=0.0 if (1401<i<n_points): A[i]=4000*sin(t[i]/200)+4000 k1_XR = func_XR_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1]) k1_CY = func_CY_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1]) k1_XRa = func_XRa_prime(t[i-1],XR[i-1],CY[i-1],XRa[i-1],A[i-1]) #first step t1 = t[i-1] + (h/2.0) XR1 = XR[i-1] + (h/2.0) * k1_XR CY1 = CY[i-1] + (h/2.0) * k1_CY XRa1 = XRa[i-1] + (h/2.0) * k1_XRa k2_XR = func_XR_prime(t1,XR1,CY1,XRa1,A[i-1]) k2_CY = func_CY_prime(t1,XR1,CY1,XRa1,A[i-1]) k2_XRa = func_XRa_prime(t1,XR1,CY1,XRa1,A[i-1]) #second step t2 = t[i-1] + (h/2.0) XR2 = XR[i-1] + (h/2.0) * k2_XR CY2 = CY[i-1] + (h/2.0) * k2_CY XRa2 = XRa[i-1] + (h/2.0) * k2_XRa k3_XR = func_XR_prime(t2,XR2,CY2,XRa2,A[i-1]) k3_CY = func_CY_prime(t2,XR2,CY2,XRa2,A[i-1]) k3_XRa = func_XRa_prime(t2,XR2,CY2,XRa2,A[i-1]) #third step t3 = t[i-1] + h XR3 = XR[i-1] + (h/2.0) * k3_XR CY3 = CY[i-1] + (h/2.0) * k3_CY XRa3 = XRa[i-1] + (h/2.0) * k3_XRa k4_XR = func_XR_prime(t3,XR3,CY3,XRa3,A[i-1]) k4_CY = func_CY_prime(t3,XR3,CY3,XRa3,A[i-1]) k4_XRa = func_XRa_prime(t3,XR3,CY3,XRa3,A[i-1]) #fourth step average_k_XR = (1.0/6.0)*(k1_XR + 2.0*k2_XR + 2.0*k3_XR + k4_XR) average_k_CY = (1.0/6.0)*(k1_CY + 2.0*k2_CY + 2.0*k3_CY + k4_CY) average_k_XRa = (1.0/6.0)*(k1_XRa + 2.0*k2_XRa + 2.0*k3_XRa + k4_XRa) t[i] = t[i-1] + h XR[i] = XR[i-1] + h * average_k_XR CY[i] = CY[i-1] + h * average_k_CY XRa[i] = XRa[i-1] + h * average_k_XRa #Plot plot(t,XR,label='XR') plot(t,CY,label='CY') plot(t,XRa,label='XRa') plot(t,A,label='A') plt.xlabel('t(min)',size=20) plt.ylabel('proteins',size=20) legend() figure(figsize(15,10)) plt.savefig("Shewanelladet.png", format='png',bbox_inches='tight',transparent=False)

Stochastic Model

Synechococcus elongatus

%pylab inline #This function 'decides' what happens in the Gillespie algorythm depending on the output of the second random number. def decider(random): if(0<=random<cltve[1]): LI.append(LI[i] + 60) XI.append(XI[i] + 60) EAi.append(EAi[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) elif(cltve[1]<=random<cltve[2] and LI[i] != 0 ): LI.append(LI[i] - 1) XI.append(XI[i]) EAi.append(EAi[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) elif(cltve[2]<=random<cltve[3] and XI[i] != 0): LI.append(LI[i]) XI.append(XI[i]-1) EAi.append(EAi[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) elif(cltve[3]<=random<cltve[5]): EAi.append(EAi[i] + 60) LI.append(LI[i]) XI.append(XI[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) elif(cltve[5]<=random<cltve[6] and EAi[i]!=0): EAi.append(EAi[i] - 1) LI.append(LI[i]) XI.append(XI[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) else: LI.append(LI[i]) XI.append(XI[i]) EAi.append(EAi[i]) CL.append(4000*sin(2*3.141592*T/1440)+4000 + r3) #The array t1 will contain all of the time intervals calculated with the tau formula t1 = [0.0] #An array for each of the protein concentrations is initialized LI = [0.0] XI=[0.0] CL=[0.0] EAi=[0.0] # All of the constants involved in the differetial equations are established here aCL = 0.0 bCL = 5.0 nCL = 2.0 kCL = 3000.0 gXI = 0.033 gLI = 0.033 aL = 1.0 bL = 5.0 kL = 3000.0 nL = 2.0 gEAi = 0.033 # This for loop iterates for 800'000 events. Each run-through, a time interval is calculated and added #to the time array and each protein array is updated. for i in range(800000): ks=[] cltve=[] #LI events k0 = aCL k1 = ((bCL*pow(CL[i],nCL))/(pow(CL[i],nCL)+pow(kCL,nCL))) k2 = gLI*LI[i] ks.append(k0) ks.append(k1) ks.append(k2) #XI Events k3 = gXI*XI[i] ks.append(k3) #EAi Events k4 = aL k5 = (bL/(1+pow((LI[i]/kL),nL))) k6 = gEAi*EAi[i] ks.append(k4) ks.append(k5) ks.append(k6) #s will represent the sum of all events s=0 for j in ks: s = s+j for j in range(len(ks)): if(j==0): cltve.append(ks[0]/s) else: cltve.append(cltve[j-1] + ks[j]/s) r1 = random.random() #We calculate the time interval for the next event to happen T = (1/s)*log(1/r1) + t1[i] #The time interval is added to the time array t1.append(T) #This random number will decide which event is chosen. r2 = random.random() #This random number is used to generate some noise in the input signal. r3 = (random.random()*1000)-500 #This recalls the function to decide which event happens. decider(r2) figure(figsize(15,10)) plot(t1,CL,label='CL') plot(t1,XI,label='XI') plot(t1,LI,label='LI') plot(t1,EAi,label='EAi') plt.xlabel('Time (mins)', fontsize = 20) plt.ylabel('# of molecules' , fontsize = 20) plt.title('Stochastic simulation', fontsize = 30) legend(fontsize = 15) savefig('cyano.png') show()

Shewanella oneidensis

%pylab inline #We initialize the time array t2, the arrays for proteins and establish #the constants that will be used in the equations. t2 = [0.0] XR = [0.0] XR2 = [0.0] CY =[0.0] A = [0.0] aXR = 10 bXR = 5.0 kXR = 3000.0 gXR = 0.033 dXR2 = 0.1998 gXR2 = 0.033 aX = 10 bX = 100 nX = 2.0 kX = 10000 gCY = 0.25 kr1 = 0.00015 # This for loop iterates for 800'000 events. Each run-through, a time interval is calculated and added #to the time array and each protein array is updated. for i in range(12800000): ks=[] cltive=[] #XR events k0 = aXR k1 = kr1*XR[i]*A[i] k2 = gXR*XR[i] k3 = dXR2*XR2[i] ks.append(k0) ks.append(k1) ks.append(k2) ks.append(k3) #XR2 events k4 = gXR2*XR2[i] ks.append(k4) #CY events k5 = aX k6 = (bX*pow(XR2[i],nX))/(pow(kX, nX) + pow(XR2[i],nX)) k7 = gCY*CY[i] ks.append(k5) ks.append(k6) ks.append(k7) #s will represent the sum of all events s = 0 for j in ks: s = s+j for j in range(len(ks)): if(j==0): cltive.append(ks[0]/s) else: cltive.append(cltive[j-1] + ks[j]/s) r1 = random.random() #We calculate the time interval for the next event to happen T = (1/s)*log(1/r1) + t2[i] #The time interval is added to the time array t2.append(T) #This random number will decide which event is chosen. r2 = random.random() #This function 'decides' what happens in the Gillespie algorythm depending #on the output of the second random number. def decider(random): if(0<=random<cltive[0]): XR.append(XR[i] + 60) XR2.append(XR2[i]) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[0]<=random<cltive[1] and XR[i] != 0): XR.append(XR[i] -1 ) XR2.append(XR2[i] + 1) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[1]<=random<cltive[2] and XR[i] != 0): XR.append(XR[i] - 1) XR2.append(XR2[i]) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[2]<=random<cltive[3] and XR2[i] !=0): XR.append(XR[i] +1) XR2.append(XR2[i] -1) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[3]<=random<cltive[4] and XR2[i] !=0): XR.append(XR[i]) XR2.append(XR2[i] -1) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[4]<=random<cltive[5]): XR.append(XR[i]) XR2.append(XR2[i]) CY.append(CY[i] + 60) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[5]<=random<cltive[6]): XR.append(XR[i]) XR2.append(XR2[i]) CY.append(CY[i] +60) A.append(4000*sin(2*3.141592*T/1440)+4000) elif(cltive[6]<=random<cltive[7] and CY[i] != 0): XR.append(XR[i]) XR2.append(XR2[i]) CY.append(CY[i] - 1) A.append(4000*sin(2*3.141592*T/1440)+4000) else: XR.append(XR[i]) XR2.append(XR2[i]) CY.append(CY[i]) A.append(4000*sin(2*3.141592*T/1440)+4000) #This recalls the function to decide which event happens. decider(r2) figure(figsize(15,10)) plot(t2,XR,label='XR') plot(t2,XR2,label='XR*') plot(t2,CY,label='CY') plot(t2,A,label='AHL') plt.xlabel('Time(mins)' , fontsize = 20) plt.ylabel('# of molecules', fontsize = 20) plt.title('Stochastic Simulation', fontsize = 30) legend(fontsize = 10) savefig('shewanellaestocasbX40.png') show()

Uploading pictures and files

You can upload your pictures and files to the iGEM 2015 server. Remember to keep all your pictures and files within your team's namespace or at least include your team's name in the file name.
When you upload, set the "Destination Filename" to Team:YourOfficialTeamName/NameOfFile.jpg. (If you don't do this, someone else might upload a different file with the same "Destination Filename", and your file would be erased!)

CLICK HERE TO UPLOAD FILES