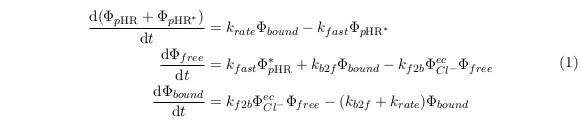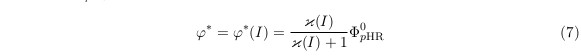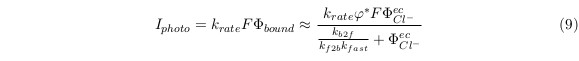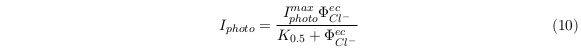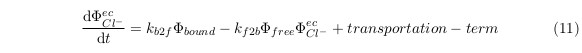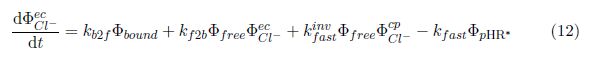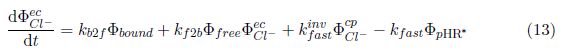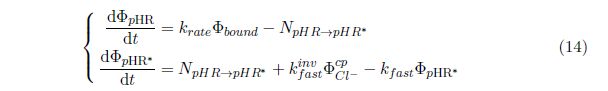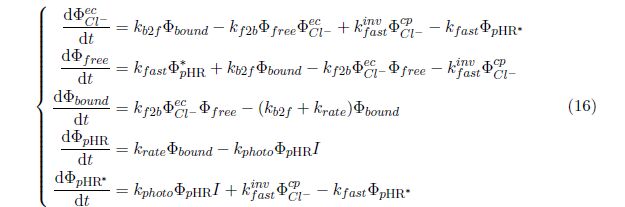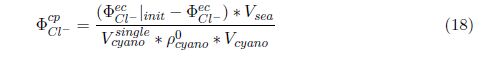Modeling
Contents
Introduction
Overview
This report is trying to give a qualitative description of our team’s desalination tool. Before we enter the modelling part of this report, I want to give some basic ideas of our team’s project and some mathematical tools I will use during the modelling. Our team’s project focuses on the worldwide problem-shortage of fresh water. We try to modify the cyanobacterium via the methods and tools of biosynthesis. We want to im-plant the Natronomonas pharaonis halorhodopsin(pHR), which is an archaeal rhodopsin functioning as an inward-directed, lightdriven Cl− pump, into the cyanobacterium. We want to use this protein carried by cyanobacterium and driven by light energy to desalinate the sea water. That’s the very general idea of our project. At the meantime, we modify the corresponding promoter of pHR which makes the expression of pHR inhibited in dark environment. Such a promoter is just like a switch which could control the expression of pHR by the environment. Then, the whole working landscape of our modified cyanobacterium could be divided as following steps:
- Natural Growth
- Dark Expression
- Starving Working
I will explain each process in detail in the following sections. <math>\phi</math>
Natural Growth Process
This process is just as straight forward as its name. In this process, we need our modified cyanobacterium grows naturally to a appropriate population number. The process is mainly determined by the target volume of sea water. It is plain in experiment sense. However, in modelling sense, we need a growth model to describe this process or have a method to measure the density in the end of this process. The reason I will explain later.
Dark Expression Process
In dark expression process, we put our modified cyanobacterium in dark environment. The duration of this process will directly affect the expression level of pHR. The expression level of pHR is critical for the next stage and modelling. In this process, we also need a dark expression model or a method to measure the average expression level of pHR in the end of this process because of the same reason as natural growth process.
Starving Working Process
Starving working process is the most important one. In this process, we need our modified cyanobacterium been in starving status. Then, provided with specific wavelength 3light, the pHR could tranport the Cl− against the gradient of Cl− concentration and reach the purpose of desalination.
Modeling Intro.
As you can see, our team’s project involves a seris of processes. A complete modelling of our bio-system should at least consist of three model: growth model, dark expression model and starving working model. However, it is not necessary and also not wise to model all process one by one. Our focus should put on the last process-starving working process but it is obvious that the result of previous process could affect the fianl process significantly. Thus some parameters in the model of last process, we need obtain by experiment methods. Here I list some parameters reserved for previous process or outside environment:
- The density of cyanobacterium
- The expression level of pHR
- The intensity of light
- The initial concentration of Cl−.
Modeling
Before we begin our modelling work, we need to make our aim clear. The reason of modelling is we want to use the intrinsic logic of mathematics to reveal the still uncler part in this relevant problem. However, the very difficult part in modelling biosystem is the biosystem is a complex system. The varibles and processes involved are complicated to consider. In our project, the very first thing we need to unstand is what happened in the starving working process? This part we mainly rely on the published papers\xe2\x80\x99 results. Only when we have some basic ideas about this process, we can do something more. Then, we need to choose mathematical tools to describe our model. In our problem, the process is very mysterious for us and not easy to describe quantitatively. But we know that no matter how complicated the process is, some fundamental laws must obey. If we see our problem in microscopic level, this process should dominate by electromagnetic law. Therefore, the method of molecular dynamics could be applied. But the computation cost is not affordable, the accuracy is not suitable for our purpose and the method is too difficult for us. Then we need to simplify the problem. In order to achive this, rise the observation level a little highter. We choose the very fundamental law-conservation law.
Assumptions
As I have mentioned before, our model will based on conservation law. I choose to model our system in a very simple case in macroscoplic level as our fisrt simple model. To achive this, I need some assumptions.
- The cyanobacterium density is not too high, then each cyanobacterium could be regareded as independent one.
- During starving working process, once provided continous illuminations, each reactions in this process reach equilibrium quickly.
- Ignore the spatial distribution of concentrations or other possible quantities. Assume these quantities is sufficiently homogeneous.
- Assume the effect of each cyanobacterium could be linear superposition.
Variables
- The extracelluar concentration of Cl−: Φ Cl− ec
- The cytoplasmic concentration of Cl−: Φ Cl− cp
- The light intensity: I
- The pHR expression level: Φ pHR 0
- The cyanobacterium density: ρ cyano 0
- The volume of cyanobacterium growth medium: V cyano
- The volume of a single cyanobacterium: V cyano single
- The volume of target sea water: V sea
- The Cl − -free intermediate concentration: Φ free
- The Cl − -bound intermediate concentration: Φ bound
- The concentration of original pHR: Φ pHR
- The concentration of excited pHR: Φ pHR ∗
- The chemical reaction constant of fast transition process: k fast
- The chemical reaction constant of rate determining process: k rate
- The chemical reaction constants of intermediate reaction: k f2b , k b2f
- The proportiality of pHR to pHR� process: k photo
- The concentration of all pHR involved in the photoinduced cycle: φ ∗
- The ratio of excited pHR to unexcited pHR: κ
Details
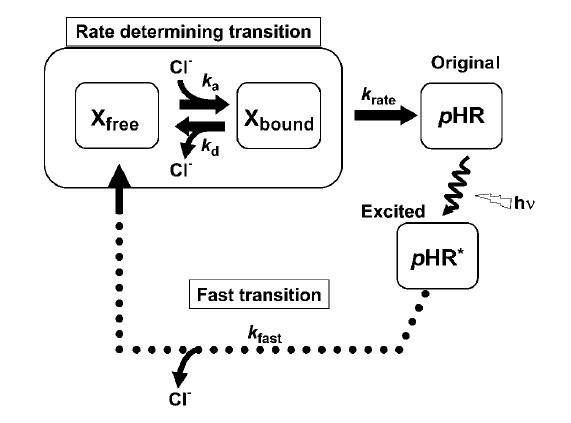
The detail of our model will be explained in this part. The process division is mainly based on published paper result. As shown in the figure 5.1.1, the whole cycle in this process could be divided into two parts: one is the fast transition of intermediates corresponding to Cl− translocating and releasing processes, and the other is the rate-determining transition corresponding to Cl− binding processes. Use the law of mass action in chemical reaction theory, we could have following equations:
Note that the total amount of pHR φ∗ involved in the photoinduced current cycle is:
With our previous assumptions, all reaction processes reach equilibrium quickly under continuous illumination. Thus all left side of above equations could approximate by zero. Then solve these equation system, we could find that:
We also have that the conserved quantity-the pHR expression level: Φ0pHR , which equals to:
where φ∗ is determined by dark expression process. According to the experiment result, we note that the excited pHR concentration φ∗ should be a function of light intensity I, i.e.
In order to write this relation explicitly, we rewrite the excited pHR concentration φ∗ :
where κ = φ∗ / ΦpHR . Therefore, the effect of light intensity could be writtten as:
The relation between excited to unexcited ratio κ and light intensity I should be determined by experiment or other methods.
If we consider the photoinduced current Iphoto , we could obtain that:
where F is the Faraday’s constant. Note that k rate is much smaller than any other constants. Then we can do some simplification.
Let Iphotomax = krate φ∗ F , thus the equation could be reduced as the form of Michaelis-Menten-type equation:
Until now, we have made a progross but still far away from solving the problem. Remember that all these results are based on fast equilibrium approximation. This approximation gives us some good results but also trobles. If we want to model the whole process of our system, how could we just consider the situation in equilibrium? Only the results in equilibrium situation is not sufficient to predict the behaviors of this complex system.
Now consider the change of concentration of Cl− in non-equilibrium situation.
where the transportation term is used for describing the pHR active Cl− transport process. However, this term is not easy to write explicitly. If we divide the non-equilibrium process into small time segment and regard each segment as quasi-equilibrium, we could use the previous equilibrium results to describe the transpotation effect, i.e.
However, here is another thing peculiar we should pay attention to. The active trans-
potation carried by pHR protein pHR ∗ → Clcp- + Intfree process should be mainly affected by the concentration of Cl-. Then, I simply wrap out Φfree in the transportation term.
Consider the photoreaction process which activates the original state pHR to active state pHR ∗.Note the figure 1, we could write following equations:
where the term N pHR → pHR ∗ stands for the number of pHR ∗ converted from original pHR in unit time in photoreaction process. However, this effect is not easy to describe explicitly just as the effect of light intensity upon photoinduced current which has been mentioned before. In order to proceed, I will add another two assumptions for the photoreaction process which are:
- Photoreaction rate is propotional to the concentration of pHR, i.e. N pHR → pHR ∗ / ΦpHR
- Weak illumination assumption. Under this assumption, it's reasonable to assume that photoreaction rate is proportional to the intensity of illumination, i.e. N pHR → pHR ∗ / I
With these two assumptions, the term N pHR → pHR ∗ could be denoted as:
Please note that the proportional constant k photo is not the meaning of reaction constant. Combine with other two obvious equations, we can obtain the final equation system:
However, until now it is still insuffi�cient to solve this equation system. There are six unknows: Φ Cl− ec , Φ bound , Φ free , Φ pHR , Φ pHR ∗ and Φ Cl− cp while only �five independent equations. We still need one more equation. Now it's time to use the conservation law of Cl - , i.e.
Do some simple calculations, we obtain that
Then, substitute this equation into above equation system,
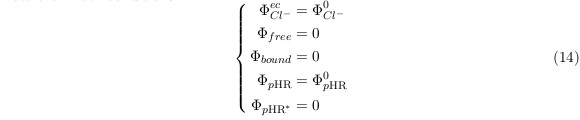
Note the initial conditions:
Theoretically speaking, we can solve this system to simulate the process and predict the concentration of Cl− . The simulation result will present in the next section.
Simulation
Conclusion
Reference
[1] Heterologous Expression of Pharaonis Halorhodopsin in Xenopus laevis Oocytes and Electrophysiological Characterization of Its Light-Driven Cl− Pump Activity Akiteru Seki et al. Biophysical Journal Volume 92 April 2007 2559–2569 2559
[2] Mathematical Physiology James Keener James Sneyd ISBN 978-0-387-75846-6