Team:Waterloo/Modeling/CaMV Replication
CaMV Replication
Model Formation
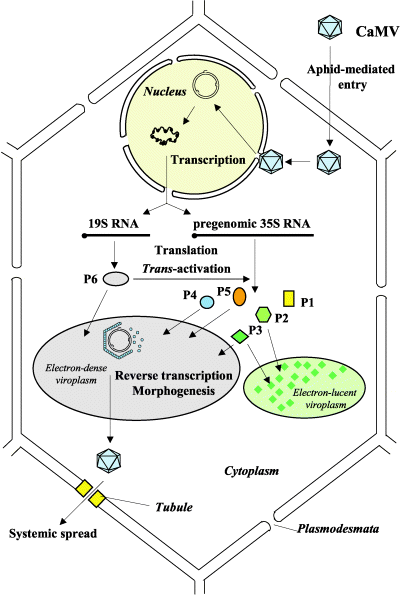
There are several core processes involved in CaMV replication within an infected host cell. The details of CaMV replication are discussed on the CaMV Biology page and shown in the figure. In brief, however, we determined that in addition to typical processes such as transcription, constitutive translation, and degradation we must also account for the following processes in our model:
- Virions reinfecting the nucleus
- Repair of pdsDNA
- Splicing of 35S RNA
- RNA interference
- Packaging of 35S RNA
- P6 transactivating production of P1-P5
- Anchoring of P3 to the viral capsid
- Virions exiting the cell
Additionally, since our project uses CRISPR to produce a targeted mutation in the P6 gene, we track both wild-type and mutated versions of genomes, pregenomes, and virions.
- Photo © Haas et al. (2005)
- Figure 3 of Cauliflower mosaic virus: still in the news
Network and Equations
We should add in a diagram of our network. Someone pls draw this k thx. I think we shoul
DNA
$$\frac{d d_g}{dt} = k_v V (d_{max} - d_{total}) - \alpha_c d_g - k_g d_g - \gamma_d d_g$$ $$\frac{d d_c}{dt} = \alpha_c d_g - k_c d_c - \gamma_d d_c$$ $$\frac{d d_{gm}}{dt} = k_v V_m (d_{max} - d_{total}) - \alpha_c d_{gm} + k_g d_g - \gamma_d d_{gm}$$ $$\frac{d d_{cm}}{dt} = \alpha_c d_{gm} + k_c d_c - \gamma_d d_{cm}$$
RNA
$$\frac{d r_{19S}}{dt} = \alpha_{19S} d_c - (\gamma_{19S}+\gamma_{r}) r_{19S}$$ $$\frac{d r_{35S}}{dt} = \alpha_{35S} d_c - k_p p_4 p_5 f_u r_{35S} - (\gamma_{35S}+\gamma_{r}) r_{35S}$$ $$\frac{d r_{35Sm}}{dt} = \alpha_{35S} d_{cm} - k_p p_4 p_5 f_u r_{35Sm} - (\gamma_{35S}+\gamma_{r}) r_{35Sm}$$
Protein
$$\frac{d p_3}{dt} = \beta_3 \left( \frac{p_6}{p_6+K_6} \right) (r_{35S} + r_{35Sm}) - k_a p_3 (V_i+V_{im}) - \delta_3 p_3$$ $$\frac{d p_4}{dt} = \beta_4 \left( \frac{p_6}{p_6+K_6} \right) (r_{35S} + r_{35Sm}) - k_p p_4 p_5 f_u (r_{35S} + r_{35Sm}) - \delta_4 p_4$$ $$\frac{d p_5}{dt} = \beta_5 \left( \frac{p_6}{p_6+K_6} \right) (r_{35S} + r_{35Sm}) - k_p p_4 p_5 f_u (r_{35S} + r_{35Sm}) - \delta_5 p_5$$ $$\frac{d p_6}{dt} = \beta_6 r_{19S} - \delta_6 p_6$$
Virions
$$\frac{d V_i}{dt} = k_p p_4 p_5 f_u r_{35S} - k_a p_3 V_i$$ $$\frac{d V}{dt} = k_a p_3 V_i - k_v V (d_{max} - d_{total}) - v_e V - \delta_v V$$ $$\frac{d V_{im}}{dt} = k_p p_4 p_5 f_u r_{35Sm} - k_a p_3 V_{im}$$ $$\frac{d V_m}{dt} = k_a p_3 V_{im} - k_v V_m (d_{max} - d_{total}) - v_e V_m - \delta_v V_m$$
Algebraic Equations
$$d_{total} = d_g + d_c + d_{gm} + d_{cm}$$ $$\gamma_r = \frac{L}{1+e^{k (p_6-x_0)}}$$ $$x_0 = \frac{1}{2} p_6 ^{ss}$$ $$p_6 ^{ss} = \frac{\beta_6}{\delta_6} \frac{\alpha_{19}}{\gamma_{19}} d_{max}$$
- Cell concentrations are continuous
- Molecules in the cytosplasm are well-mixed
- No outside infection
- This ODE model only tracks replication within one cell, it cannot track multiple cells. This is handled by the viral spread model instead
- Limited number of genomes in nucleus
- "Another pool of viral genomes, in the order of 10-100 copies of minichromosomes comprising supercoiled circular viral DNA and host histones, accumulates in the nucleus."
- Rate of repair of gapped DNA follows law of mass-action
- Rate of P6 gene mutation is proportional to number of wild-type genomes
- DNA, RNA, proteins, and complete virions degrade, incomplete virions do not
- We assume P3 binds to virions rapidly enough for incomplete virion degradation to be negligible
- We are only targeting 19S RNA
- RNA production follows mass-action
- Concentration of spliced/unspliced RNA is at rapid equilibrium
- Spliced and unspliced 35S RNA degrade at the same rate
- Encapsidation and reverse transcription occur simultaneously
- Information for CaMV is lacking, but for HBV (another pararetrovirus) reverse transcription is initiated during encapsidation and encapsidation is initiated by RT . The complexity of this packaging process is not fully captured in this model
- Only unspliced RNA is packaged
- Spliced RNA lacks P1 and P2 and so, although able to replicate within the cell, virions which package spliced RNA will be unable to propagate
- P1 and P2 do not affect replication dynamics
- P1 is primarily involved in cell-to-cell movement and P2 with host-to-host movement. Neither have a significant impact on the replication process
- P6 is only translated from 19S RNA, translation rate is proportional to cccDNA copy number
- P3, P4, and P5 are translated from 35S RNA, translation is activated by P6
- This is very well established
- All P6 is incorporated in inclusion bodies
- Mass-action anchoring of P3 to virions
- All P4 is instantaneously spliced
- As discussed above the subtleties of encapsidation are not captured by this model
- Virions may reinfect nucleus
- This is very well established
- Virions leave the cell at a constant rate
Model Parameters
Finding and implementing accurate parameter values is crucial when trying to draw conclusions from a model. Our model contains nearly thirty parameters, each of which needed to be found to exactly reproduce the viral replication process in silico. Model dynamics may be drastically affected by our choice in parameters and this must be accounted for in our analysis. However, as with many models in systems biology our network suffers from the "parameter problem" described in chapter 1 of the book by Gunawardena which arises from the complexity of biological processes and the difficulty in measuring parameter values.
A number of parameter values are the same as those used in an HBV model developed by Nakabayashi & Sasaki . Parameters that have a reference in the "Source" column are ones we were able to find or derive accurate values for from the literature. Unfortunately, there are a few parameter values that could not be found (e.g. the half-saturation constant of P6 activation) and so we explicitly mention the absence of data in the table. In order to compensate for the lack of accurate parameters, we analyze our model over a wide range of parameters to determine how behaviour will be affected. Lastly, for simplicity we normalized each concentration by the volume of the cell (volume=1.414x10$^{-13}$m$^3$).| Symbol | Value | Units | Description | Source |
|---|---|---|---|---|
| $k_v$ | 0.1 | min$^{-1}$ | Rate at which virions produced by the cell reinfect the nucleus. | No source found, parameter is further analyzed in the results section |
| $d_{max}$ | 100 | molecules/volume | Maximum concentration of viral genomes in the nucleus. | "Another pool of viral genomes, in the order of 10-100 copies of minichromosomes comprising supercoiled circular viral DNA and host histones, accumulates in the nucleus" |
| $\alpha_c$ | 0.1 | min$^{-1}$ | Rate at which gaps are repaired in gapped DNA to form cccDNA. | HBV model by Nakabayashi & Sasaki |
| $k_g$ | 0.01 | min$^{-1}$ | Rate at which the P6 gene on the gapped DNA is modified. | No source found, parameter is further analyzed in the results section |
| $k_c$ | 0.01 | min$^{-1}$ | Rate at which the P6 gene on cccDNA is modified. | No source found, parameter is further analyzed in the results section |
| $\gamma_d$ | 0.001 | min$^{-1}$ | DNA Degradation rate. | HBV model by Nakabayashi & Sasaki |
| $\alpha_{19S}$ | 0.01 | min$^{-1}$ | Transcription rate of 19S RNA. | HBV model by Nakabayashi & Sasaki |
| $\alpha_{35S}$ | 0.05 | min$^{-1}$ | Transcription rate of 35S RNA. | HBV model by Nakabayashi & Sasaki |
| $\gamma_{19S}$, $\gamma_{35S}$ | 0.001 | min$^{-1}$ | Degradation rate of 19S RNA, 35S RNA. | HBV model by Nakabayashi & Sasaki |
| $f_u$ | 0.3 | unitless | Fraction of unspliced 35S RNA in the cell (assumed at equilibrium). | Froissart et al. 2004 <\cite> and Bouton et al. 2015 <\cite> |
| $\beta_3$, $\beta_4$, $\beta_5$, $\beta_6$ | 0.1 | min$^{-1}$ | Translation rate of P3, P4, P5, P6. | HBV model by Nakabayashi & Sasaki |
| $K_6$ | 1000 | molecules/volume | Half-saturation constant for transactivation of P1-P5 production. | No source found, parameter is further analyzed in the results section |
| $\delta_3$, $\delta_4$, $\delta_5$, $\delta_6$ | 0.001 | min$^{-1}$ | Degradation rate of P3, P4, P5, P6. | HBV model by Nakabayashi & Sasaki |
| $k_p$ | 0.1 | molecules$^{-2}$ min$^{-1}$ | Packaging rate. | No source found, parameter is further analyzed in the results section |
| $k_a$ | 7.5 x 10$^4$ (original) or 5.3 x 10$^{34}$ (converted) |
M$^{-1}$ s$^{-1}$ (original) or volume molecules$^{-1}$min$^{-1}$ (converted) | Rate of P3 anchoring to virions. | |
| $v_e$ | 0.1 | min$^{-1}$ | Rate at which virions exit the cell. | No source found, parameter is further analyzed in the results section |
| $\delta_v$ | 0.001 | min$^{-1}$ | Rate of virion degradation. | HBV model by Nakabayashi & Sasaki |
| $L$ | 0.005 | min$^{-1}$ | Maximum RNAi effectiveness. | Estimated to be on the order of $\gamma_{35S}$, but slightly larger since RNAi is more effective than degradation |
| $k$ | 10$^{-4}$ | molecules$^{-1}$ | Slope of logistic function describing RNAi effectiveness | No source found, parameter is further analyzed in the results section |
Results
Model Validation
Include notes on how the model matches reality/our expectations of reality in this section.