Difference between revisions of "Team:Cambridge-JIC/Autofocus"
KaterinaMN (Talk | contribs) |
KaterinaMN (Talk | contribs) |
||
| Line 55: | Line 55: | ||
<ul> | <ul> | ||
<li><p>Tested out focus scores based on variance since this was recommended by both sources [1][2] on artificially blurred out images (Gaussian blur with different standard deviations). This worked well. <b>Variance was chosen as the focus measure to implement since it is quick to evaluate</b> (speed being an important priority), and numpy has a function that does this already.</p></li> | <li><p>Tested out focus scores based on variance since this was recommended by both sources [1][2] on artificially blurred out images (Gaussian blur with different standard deviations). This worked well. <b>Variance was chosen as the focus measure to implement since it is quick to evaluate</b> (speed being an important priority), and numpy has a function that does this already.</p></li> | ||
| − | <li><p>Implemented an autofocus method for multiresolution search (described in the textbook [2], section 16.3.3).</p> | + | <li><p>Implemented an autofocus method for multiresolution search (described in the textbook [2], section 16.3.3).</p></li> |
| − | + | ||
<li><p>Implemented DWT (Discrete Wavelet Transform) to decompose image to low resolution versions. This was expected to allow for faster computation and autofocusing. In practice, there was no significant computational advantage from this, so low-res images were not used in the final algorithm.</p></li></ul> | <li><p>Implemented DWT (Discrete Wavelet Transform) to decompose image to low resolution versions. This was expected to allow for faster computation and autofocusing. In practice, there was no significant computational advantage from this, so low-res images were not used in the final algorithm.</p></li></ul> | ||
| Line 72: | Line 71: | ||
<li><p>Implemented the Fibonacci search algorithm. It turns out that this is the optimal search algorithm for the situation of unimodal functions [2].</p></li> | <li><p>Implemented the Fibonacci search algorithm. It turns out that this is the optimal search algorithm for the situation of unimodal functions [2].</p></li> | ||
<li><p>Implemented the parabola approximation to find in focus position. </p></li> | <li><p>Implemented the parabola approximation to find in focus position. </p></li> | ||
| − | </ul></li | + | </ul></li> |
<p>Gradient search, which is a simple technique to locate local extrema, was also attempted, but did not give satisfactory results, as the learning rate required for convergence was slow. Also, noise from images drastically disrupted the calculations. This was a significant problem even when the gradient was calculated by taking multiple pictures around the point of interest. </p> | <p>Gradient search, which is a simple technique to locate local extrema, was also attempted, but did not give satisfactory results, as the learning rate required for convergence was slow. Also, noise from images drastically disrupted the calculations. This was a significant problem even when the gradient was calculated by taking multiple pictures around the point of interest. </p> | ||
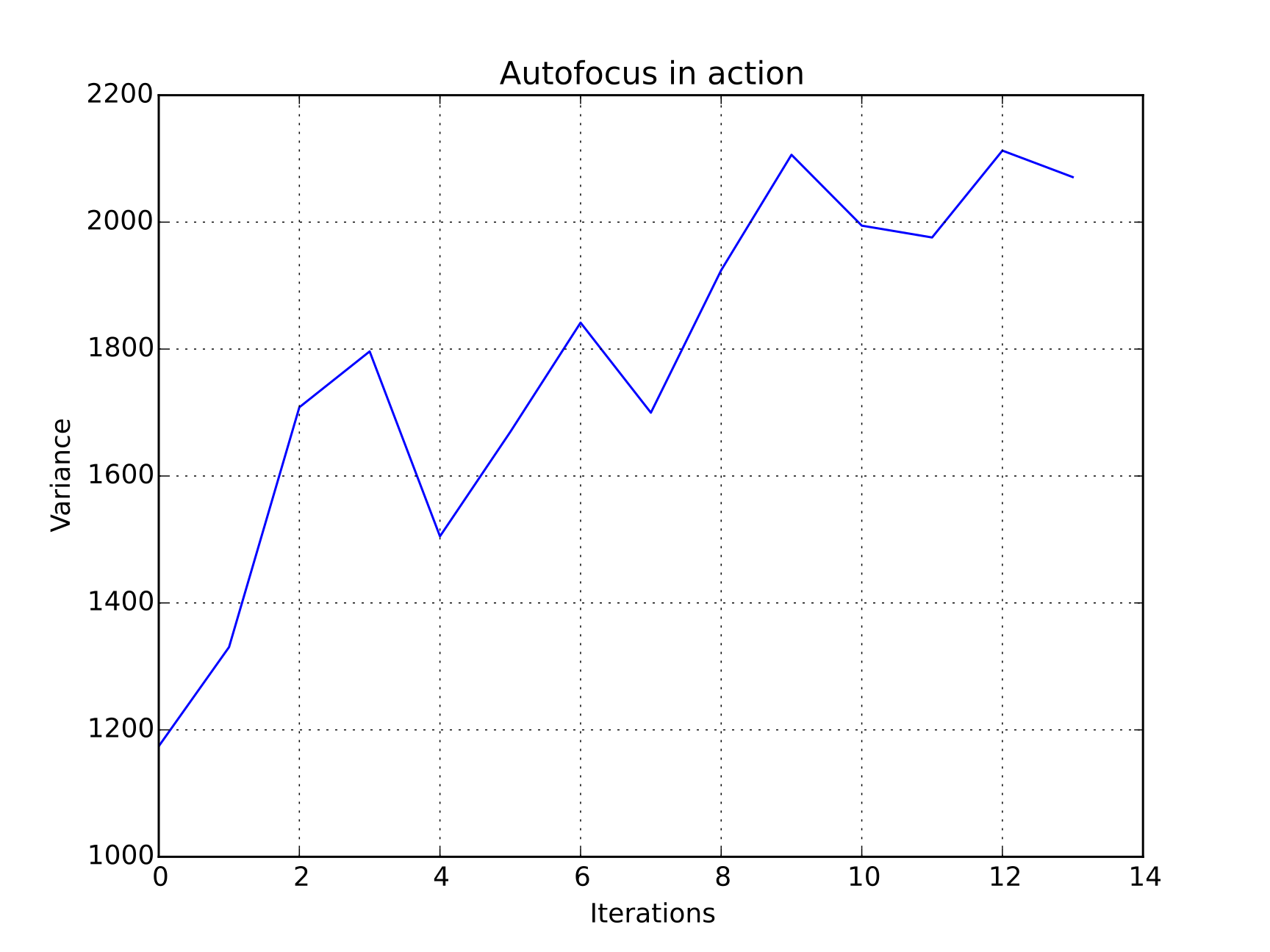
<center><img src="//2015.igem.org/wiki/images/d/da/CamJIC-Software-Autofocus-Example.jpg" style="width:40%;margin:10px"><img src="//2015.igem.org/wiki/images/b/b1/CamJIC-Software-Autofocus-Graph.png" style="width:40%;margin:10px"><p><i>Autofocus algorithm in action: the plot shows the increase of the variance (i.e. the focus score) of the image with each iteration.</i></p></center> | <center><img src="//2015.igem.org/wiki/images/d/da/CamJIC-Software-Autofocus-Example.jpg" style="width:40%;margin:10px"><img src="//2015.igem.org/wiki/images/b/b1/CamJIC-Software-Autofocus-Graph.png" style="width:40%;margin:10px"><p><i>Autofocus algorithm in action: the plot shows the increase of the variance (i.e. the focus score) of the image with each iteration.</i></p></center> | ||
Revision as of 08:33, 18 September 2015